rachunek róźniczkowy
mikejjla: | | 3x2 | |
Wyznacz zbiór wartości funkcji f(x)= |
| |
| | x2+2x+4 | |
Czy tutaj wystarczy wyznaczyć pochodną i extrema czy asymtoty też? Bo właśnie wyznaczyłam
asymtotę poziomą i wyszło mi y=3, a maximum f(−4)=4, zatem coś tu jest chyba nie tak...

. I
jeszcze mam pytanko czy gdyby było polcecenie: narysuj wykres, to gdy wyznaczałabym pochodną i
przu przyrównywaniu do 0 mam przyrównać tylko całą pochodną(wtedy mianownik nie gra roli) czy
też osobno mianownik, bo robiliśmy tak w szkole, ale jakieś to jest dziwne...
16 kwi 17:10
Janek191:
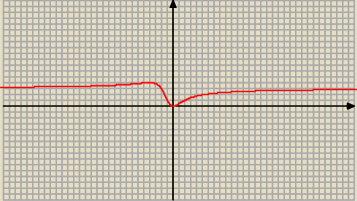
16 kwi 17:14
Janek191:
ZW = < 0, 4 >
16 kwi 17:14
mikejjla: Odpowiedź znam, ale jak do tego dojść? Teoretycznie licząc minimum i maksimum wychodzi taki
wynik, ale co z tymi asymptotami? I wiesz może jak to jest z tym przyrównywaniem do 0
pochodnej?
16 kwi 17:18
Janek191:
Pochodną przyrównuje się do 0 przy wyznaczaniu ekstremów funkcji.
16 kwi 17:20
mikejjla:
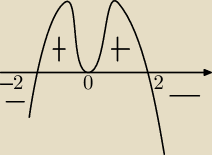
I jeszcze mam takie jedno pytanie: gdy mam np. taki wykres pochodnej, to przy opisywaniu
f'(x)>0 dla x∊(−2;2) czy dla x∊(−2;2)\{0}

?
Przepraszam za ten koślawy wykres, ale jeszcze nie do końca potrafię tutaj rysować

16 kwi 17:25
Janek191:
f '(x) > 0 dla x ∊ ( − 2, 0) ∪ ( 0, 2)
16 kwi 17:28
mikejjla: tak wiem, ale np. jakby było polecenie: naszkicuj wykres funkcji, to wtedy wyznacza się te
asymptoty itd. i między innymi wyznacza się też extrema i gdybym miała pochodną:
| | 6x2+24x | |
|
| to przy porównaniu do 0, moge pomnożyć przez mianownik, czyli |
| | (x2+2x+4)2 | |
w sumie mam 6x
2+24x=0, a my w szkole właśnie przy szkicowaniu wykresów takich funkcji,
robiliśmy tak: 6x
2+24x=0 i (x
2+2x+4)
2=0, czy można tak robić?
16 kwi 17:29
mikejjla: okej, dziękuję

To jeszcze jedno pytanie

Gdy są zadania optymalizacyjne i wyznacza się do nich dziedzinę, to wtedy uwzględnia się ją
przy rysowaniu pochodnej, czy tylko gdy się już wyznacza gdzie funkcja rośnie, a gdzie maleje?
16 kwi 17:30
Janek191:
Mianownik pochodnej jest liczbą > 0 dla x ∊ Df
Zajmujemy się tylko licznikiem .
16 kwi 17:33
mikejjla: tak właśnie myślałam, a my przy wszystkich zadaniach tego typu, tak robiliśmy..., dobra,
dziękuję bardzo za pomoc

16 kwi 17:37
 . I
jeszcze mam pytanko czy gdyby było polcecenie: narysuj wykres, to gdy wyznaczałabym pochodną i
przu przyrównywaniu do 0 mam przyrównać tylko całą pochodną(wtedy mianownik nie gra roli) czy
też osobno mianownik, bo robiliśmy tak w szkole, ale jakieś to jest dziwne...
. I
jeszcze mam pytanko czy gdyby było polcecenie: narysuj wykres, to gdy wyznaczałabym pochodną i
przu przyrównywaniu do 0 mam przyrównać tylko całą pochodną(wtedy mianownik nie gra roli) czy
też osobno mianownik, bo robiliśmy tak w szkole, ale jakieś to jest dziwne...

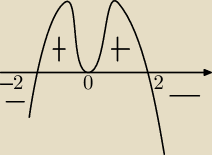 I jeszcze mam takie jedno pytanie: gdy mam np. taki wykres pochodnej, to przy opisywaniu
f'(x)>0 dla x∊(−2;2) czy dla x∊(−2;2)\{0}
I jeszcze mam takie jedno pytanie: gdy mam np. taki wykres pochodnej, to przy opisywaniu
f'(x)>0 dla x∊(−2;2) czy dla x∊(−2;2)\{0}  ?
Przepraszam za ten koślawy wykres, ale jeszcze nie do końca potrafię tutaj rysować
?
Przepraszam za ten koślawy wykres, ale jeszcze nie do końca potrafię tutaj rysować 
 To jeszcze jedno pytanie
To jeszcze jedno pytanie  Gdy są zadania optymalizacyjne i wyznacza się do nich dziedzinę, to wtedy uwzględnia się ją
przy rysowaniu pochodnej, czy tylko gdy się już wyznacza gdzie funkcja rośnie, a gdzie maleje?
Gdy są zadania optymalizacyjne i wyznacza się do nich dziedzinę, to wtedy uwzględnia się ją
przy rysowaniu pochodnej, czy tylko gdy się już wyznacza gdzie funkcja rośnie, a gdzie maleje?
