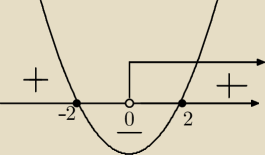
rachunek różniczkowy mikejjla: Udowodnij, że funkcja f(x)=x+4+⁴_x dla x>0 przyjmuje wartości niemniejsze od 8. Zrobiłam to tak, ale nie wiem czy dobrze:

	x2+4x+4
f(x)=
	x

	x2−4
f'(x)=
	x2

x2−4
	=0
x2

(x−2)(x+2)=0 wykres f'(x)>0 dla x∊(2;∞) f'(x)<0 dla x∊(0;2) f. rośnie dla x∊<2,∞) f, maleje dla x∊(0;2> f(2)=8 − minimum, zatem Zw_f=<8;∞) Może tak być?

J: to nie prawda .. funkcja nie posiada najmniejszej wartości , natomiast posiada minium lokalne : f(2) = 8 oraz maksimum lokalne : f(−2) = 0

PW: Dla nieujemnych a,b,c,d a+b+c+d ≥ 4³√abcd (nierówność między średnią arytmetyczną a geometryczną dla 4 elementów). Równość ma miejsce wtedy i tylko wtedy, gdy a=b=c=d.

	4
x + 2 + 2 +		≥ 43√x·2·2·4x = 44√16 = 8.
	x

Równość ma miejsce wtedy i tylko wtedy, gdy

	4
x = 2 =		⇔ x = 2.
	x

mikejjla: czyli jak zrobić to zadanie? trudno jest mi zrozumieć to minimum, maksimum itd., jak jest ekstremum to wtedy funkcja zmienia się z rosnącej na malejącą albo odwrotnie, tak?

J: no to policzmy np. f(−1) = −1 + 4 − 4 = − 1 < 8 przy x → 0 f(x) → − ∞ , więc nie ma najmniejszej wartości

J: upss ... .teraz doczytałem, że dla x > 0 .... okej w tym przedziale posiada minium lokalne: f(2) = 8

PW: J, już nie pognębiaj adeptki, w założeniu zadania jest x > 0.

mikejjla: czyli może być czy nie to rozwiązanie?

J: masz rozwiazane dobrze , liczysz ekstrema lokalne i widzisz,że dla x = 2 ( czyli:x>0) funkcja osiąga najmniejszą wartość 8 , cnw.

PW: A mój sposób jest tylko alternatywą (też dobry, ale nie wykorzystuje metod rachunku różniczkowego).

mikejjla: okej, dziękuję za poświęcenie mi czasu

J: PW ... z Twój sposób dałbym Ci 6

mikejjla: słuchajcie a jak mam takie zadanie: wyznacz te wartości parateru m, dla których prosta y=m ma co najmniej dwa punkty wspólne z wykresem funkcji y=^x3₃+x², to po wyliczeniu pochodnej, przyrównaniu do 0, wychodzi mniej więcej podobny wykres jak wyżej, tylko są inne wartości, to po naszkicowaniu wykresu gdzie maleje, gdzie rośnie, widać, że w tym przedziale między ekstremami będą co najmniej dwa punkty wspólne, więc wystarczy coś takiego czy źle?

PW: To zależy od poczucia humoru sprawdzającego. Ja też wolę rozwiązania elementarne, ale on mógłby skomentować "miała pani znaleźć ekstremum za pomocą pochodnej"

mikejjla: PW nietsety twój sposób niewiele mi mówi, już gdzieś spotkałam się z tą nierównością między średnią arytmetyczną a geometryczną, ale nie bardzo to rozumiem, w szkole też tego nie miałam, więc nie chce juz sobie mieszać w głowie, bo i tak wszystko mi się knoci . A za 6 dziękuję bardzo

mikejjla: no dokładnie i jak tu wierzyć w sprawiedliwość?

J: 6 ... przyznałem dla PW ... Ty zasłuzyłaś na 5

mikejjla: hahaaa, i tak jest dobrze

mikejjla: a z tym zadankiem z punktami wspólnymi co radzicie zrobić?

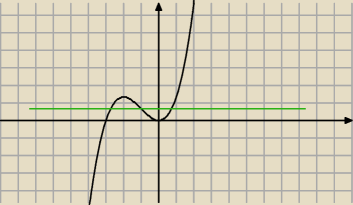
J: co do drugiego ... liczysz ekstrema lokalne, rysujesz wykres i sprawdzasz, kiedy zielona prosta ( y = m) ma co najmniej dwa punkty wspólne z wykresem

J: co najmniej , znaczy dwa lub trzy

mikejjla: tak właśnie zrobiłam, dziękuję jeszcze raz pewnie za chwilę znowu coś wrzucę, więc nie odchodźcie za daleko

PW: Oj, coś wypowiadasz się chaotycznie ... Nie pytali o iksy, lecz o wartości parametru m. Przedział będący rozwiązaniem zaczyna się w zerze, a kończy m = f_max. f{max} oznacza tu lokalne maksimum.

mikejjla: Wystarczy chyba wyliczyć f(0) i f(−2)? m∊<0;⁴₃>

J: tak