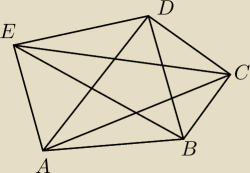
Udowodnij, że geometria Patka: Dany jest pięciokąt wypukły ABCDE: Zad.1 Udowodnij, że AC+BD+CE+DA+EB<2*(AB+BC+CD+DE+EA). Zad.2 Udowodnij, że AB+BC+CD+DE+EA<AC+BD+CE+DA+EB

YushokU: podpunkt pierwszy idzie z nierówności w trójkącie drugi z resztą też, ale trzeba trochę więcej pooznaczać na rysunku. tyle z podpowiedzi.

Patka: ok podpunkt perwszy po podpowiedzi ogarnełam nie byl trudny a co z drugim? umie mi ktos pomóc?

YushokU: Określ punkty w miejscach przecięcia sie przekątnych i myśl. Także z nierówności trojkata tylko jeden wniosek więcej

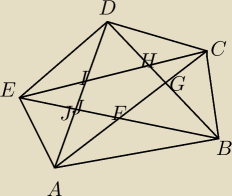
Patka: no dobra ale jak rozpisuje z równiach trójkątów wykorzystując te miejsca przecięć I J G F H to ciągle wychodzi mi to równanie wyżej jak w zadaniu tylko z przeciwnym znakiem i zawsze mam jakąś wartość więcej która mnie nie interesuje np. odcinki z oznaczeniami tych przecięć

YushokU: np. AF+FB>AB BG+GC>BC ..... i otrzymujesz (AF+GC)+(BG+HD)+(CH+IH)+(DI+JA)>AB+BC+CD+DE+EA no i teraz spójrz na rysunek. po prostu dodajesz brakujące małe odcinki do nawiasów no bo skoro a>b no to a+1>b (AF+FG+GC)+(BG+GH+HD)>AB+BC+CD+DE+EA i masz. AC+BD+CE+DA+EB>AB+BC+CD+DE+EA c.n.w.