równania ruchu
bezendu:
Qulka−fizyka
Mam wektor siły (sint, t2) i wiem, że v(0)=(0,0) i x(0)=(0,0)
obliczyć v(t) x(t) ?
15 kwi 23:18
Qulka: a masz masę?
15 kwi 23:19
bezendu:
m=1
15 kwi 23:19
Qulka: to ax=sint i ay=t2 i liczysz całki
15 kwi 23:26
bezendu:
Całkę nieoznaczoną czy oznaczoną ?
15 kwi 23:29
Qulka: nieoznaczoną, ale potem wstawiasz te zera co masz dane i liczysz stałe
15 kwi 23:51
bezendu:
Ale nawet nie wiem skąd się to wzięło, można prosić jakiś komentarz ?
16 kwi 00:01
jakubs: wiki: "Przyspieszenie definiuje się jako pochodną prędkości po czasie, czyli jest szybkością
zmiany prędkości. "
czyli: Całka z przyspieszenia to prędkość.
16 kwi 00:03
Qulka: pierwsza współrzędna to zazwyczaj x a druga y
16 kwi 00:03
bezendu:
∫sin(t)dt ?
∫t2dt ?
16 kwi 00:06
Qulka: tak
16 kwi 00:08
bezendu:
∫sin(t)dt=−cos(t)+C
I co dalej ?
16 kwi 00:14
jakubs: Podstaw za t=0, bo wiesz, że v(0)=(0,0) i wyznacz C
16 kwi 00:16
Qulka: i liczysz stałe
skoro v(0)=(0,0) to
−cos(0)+C=0 więc C=1
03/3+C=0 C=0
więc
vx=−cos(t)+1
vy=t3/3
16 kwi 00:17
Qulka: i znów całkę żeby policzyć x(t)
16 kwi 00:18
bezendu:
Nie no nie ogar a w piątek sprawdzian.
Qulka do której jesteś ?
16 kwi 00:19
16 kwi 00:21
Qulka: nie za długo bo mam już z kim spać

16 kwi 00:24
bezendu:
Dzięki, Jakub


Qulka a możesz powiedzieć po co była potrzebna masa, mam mnóstwo pytań

16 kwi 00:26
bezendu:
A jutro będziesz po południu ? W Tobie pokładam moje zaliczenie fizyki

16 kwi 00:27
jakubs: Hahaha, to widzę że sam nie jestem

Też mam koło w piątek i
Qulka jedyną nadzieją na
zdaną fizykę

16 kwi 00:28
Qulka: bo miałeś daną siłę, żeby policzyć przyśpieszenie trzeba siłę podzielić na masę
16 kwi 00:30
bezendu:
a) F→=(sin(t), t2)
b) F→=(cos(t), t3)
m=1
v(0)=(v0,0_
x(0)=(0,0)
oblicz:
v→(t)
|v→(t)|
r→(t)
|r→(t)|
r→(1)
v→(1)
16 kwi 00:38
Qulka: te z modułem to z pitagorasa
 √vx2+vy2
√vx2+vy2 i tak samo z r
16 kwi 00:42
bezendu:
Ale zobacz np teraz mam v(0)=(v0,0) czy to jest bład i powinno być v0=(0,0) ?
16 kwi 00:45
bezendu:
Qulka, może przerobimy liste zadań, a jutro wrócimy do tych równań ruchu, po południu ?
Pomożesz

?
16 kwi 00:48
bezendu:
Tych zadań nie jest dużo

16 kwi 00:49
Qulka: nie..trzeba wstawić v0
16 kwi 00:50
Qulka: dziś już idę spać..mogę zajrzeć jutro rano
16 kwi 00:51
bezendu:
ok, bardzo bym prosił o pomoc !
16 kwi 00:52
bezendu:
up
16 kwi 11:28
bezendu: ?
16 kwi 19:08
bezendu:
Pomoże ktoś ?
16 kwi 21:56
kyrtap: z czym?
16 kwi 22:10
bezendu:
Z tymi równaniami, wytłumaczy ktoś co robić po kolej ? Patrz 00:38
16 kwi 22:20
52: Ktoś tu ma jutro kartkówkę z PP

16 kwi 22:26
bezendu:
PP ?
16 kwi 22:29
52: Inicjały prowadzącego ?
16 kwi 22:30
kyrtap: Podstawowe prawo Fizyki jest zdefiniowane wzorem:
gdzie :
| | m | |
a − przyśpieszenie [ |
| ] |
| | s2 | |
F − siła [N]
m − masa [kg]
masz obliczyć V
a wiemy że prędkość jest całką drogi po czasie
tak samo droga r
całka prędkości po czasie
16 kwi 22:31
kyrtap: całkowanie wektora to nic innego jak scałkowanie każdej współrzędnej wektora
to samo z policzeniem pochodnej wektora
16 kwi 22:32
bezendu:
Ano mam z tym Panem a co też masz z nim ?
Kyrtap fb
16 kwi 22:33
52: Tak, chcesz rozwiązanie grupy B ?
16 kwi 22:34
bezendu:
Tak, poproszę

16 kwi 22:34
16 kwi 22:36
bezendu:
Już mam na grupie u Ciebie znalazłem

16 kwi 22:38
52: 
16 kwi 22:39
bezendu:
Ale to chyba nie Ty robiłeś ?
16 kwi 22:41
52: No nie, a co ?
16 kwi 22:42
bezendu:
Nic, jeszcze by się grupa A przydała

Czekajmy na Qulke
16 kwi 22:43
52: Stary robisz identycznie jak by tylko że liczysz inne całki i tyle i nie będziesz miał inne
stałe, więc nie ma na co czekać

Przecież da wam inne dane...
16 kwi 22:44
52: jak b) *
16 kwi 22:45
bezendu:
Zaraz wracam to postaram się ogarnąć.
16 kwi 22:48
kyrtap:
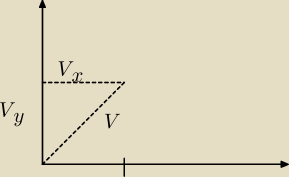
b)
F→=(cos(t), t
3)
m=1
takie mam dane wyznaczam najpierw przyśpieszenie z podstawowego prawa fizyki:
| | F→ | | [cos(t), t3] | |
a→= |
| = |
| = [cos(t),t3] |
| | m | | 1 | |
Wiemy że przyśpieszenie jest pochodną drogi po czasie, natomiast prędkość całką przyśpieszenie
po czasie. Mamy wyznaczyć prędkość a podany mamy wektor przyśpieszenia zatem:
a
→ = [cos(t),t
3] rozbijemy to na składowe wektora przyśpieszenia:
a
x = cos(t)
a
y = t
3
Liczymy całki:
składowej a
x
∫cos(t)dt = sin(t) + C
składowej a
y
otrzymaliśmy składowe więc możemy zapisać wektor prędkości
V = [V
x, V
y]
V
x = sin(t)
Czyli:
Musimy również wyliczyć moduł, moduł to nic innego jak długość przeciwprostokątnej trójkąta
prostokątnego które rozpinają ten trójkąt dwie składowe x − owa i y − owa (rysunek)
moduł ten można wyliczyć za pomocą tw. Pitagora
IVI =
√(Vx)2 + (Vy)2
16 kwi 22:50
bezendu:
kyrtap będziesz jeszcze ?

16 kwi 22:51
kyrtap: nie umiem fizyki ^^
16 kwi 22:51
Qulka: widzę że dobrze wam idzie, to mogę iść spać, bo mnie coś przewiało

16 kwi 22:53
kyrtap: wiem co to za uczucie

16 kwi 22:54
kyrtap: choruj się Qulka bo jutro zaczynamy analizę wektorową

16 kwi 22:55
Qulka: mam się bać


16 kwi 22:56
kyrtap: a tak na serio to zdrowiej i odpal sobie jakiś fajny filmik do snu

16 kwi 22:56
kyrtap: a co masz jeszcze bezendu?
16 kwi 23:01
bezendu:
Qulka zostań bo jutro kart a nic nie kumam !
16 kwi 23:19
bezendu:
F→=(cos(t), t3)
m=1
1 czemu wyznaczam przyspieszenie ?
16 kwi 23:20
kyrtap: bo siła ma ma we wzorze masę a chcemy otrzymać wektor prędkości
więc myśląc tokem fizycznym aby wyznaczyć prędkość najpierw policzymy przyśpieszenie a potem
całkując przyśpieszenie otrzymamy prędkość
16 kwi 23:33
kyrtap: tokiem*
16 kwi 23:33
bezendu:
Poczekaj 5 minut spróbuję grupę A zrobić. Widziałeś rozwiązanie w linku ?
16 kwi 23:35
kyrtap: nom widzę
16 kwi 23:37
bezendu:
v0=(v0,0) i wgl r(t) ?
16 kwi 23:39
kyrtap: wnioskuje że Vo to prędkość początkowa a r(t) droga
drogę musisz jeszcze raz scałkować
16 kwi 23:47
bezendu:
ale co tu całkować , dwa Qulka wyliczała wczoraj jeszcze stałe, Ty tego nie robisz w swoim
rozwiązaniu ?
16 kwi 23:49
kyrtap: bo nie zauważyłem tak musisz policzyć stale
16 kwi 23:53
bezendu:
2. co mam potem całkować ?
16 kwi 23:54
kyrtap: ten wektor prędkości aby otrzymać r(t)
16 kwi 23:55
bezendu:
F
→=(sin(t), t
2)
m=1
v(0)=(v0,0)
x(0)=(0,0
od początku
a=U{F}}{m}
a=[sin(t), t
2]
a
x=sin(t) a
y=t
2
∫sin(t)dt=−cos(t)+C
Co potem ?
16 kwi 23:59
kyrtap: otrzymałeś składowe Vx i Vy i wiesz z danych że V(0) = (0,0)
więc podstawiasz 0 do całek i przyrównujesz do 0 aby otrzymać składowe wektora V
17 kwi 00:01
kyrtap: bo nie możesz składowych ze stałą w wektorze zapisać one muszą być liczbą konretną
17 kwi 00:04
bezendu:
−cos(0)+C=0 c=−1
tak ?
17 kwi 00:04
kyrtap: C= 1 bo cos(0) = 1
− 1 + C = 0 ⇒ C =1
17 kwi 00:07
kyrtap: druga dobrze
17 kwi 00:07
bezendu:
ok, mam stałe i co dalej nauczycielu ?
17 kwi 00:10
kyrtap: znowu policzyć całkę z tych składowych prędkości żeby otrzymać r(t)
17 kwi 00:16
bezendu:
całkę z ?
−∫cos(t)dt=
17 kwi 00:21
17 kwi 00:24
kyrtap: tak

17 kwi 00:24
kyrtap: i teraz się zastanawiam bo tam napisałeś x = (0,0) jakby to było r = (0,0) to w łatwy sposób by
się wyznaczyło stałe co za tym idzie stałe
17 kwi 00:25
bezendu:
i co dalej bo już chyba pojamju

17 kwi 00:26
bezendu:
no tak jest nawet w linku
17 kwi 00:26
kyrtap: bo to proste masz
droga −−−−> (pochodna) prędkość −−−−−−−>(pochodna) przyśpieszenie
droga <−−−−−(całka) prędkość <=====całka przyśpieszenie
nie możesz przejść od razu z przyśpieszenia do drogi musisz dwa razy policzyć pochodną
17 kwi 00:28
kyrtap: nie wiem co by powiedziała Qulka ale mi się wydaje że to r a nie x
17 kwi 00:30
bezendu:
Czyli co dalej, chcę w końcu dokończyć i iść spać

17 kwi 00:31
kyrtap: jeżeli r(0) = (0,0)
to musisz podstawić tak jak wcześniej do tych całek aby wyliczyć stałe i po kłopocie

17 kwi 00:37
bezendu:
znowu stałe, ok
−sin(0)+C=0 C=0
i ?
17 kwi 00:40
kyrtap: i finito
17 kwi 00:42
kyrtap: już r(1) i V(1) chyba dasz radę policzyć?
17 kwi 00:42
bezendu:
Tak, dzięki skoczę jeszcze jutro do A.Mit... bo ma jutro ćw to 15 minut mu zajmę po ćw

17 kwi 00:46
kyrtap: pewnie

17 kwi 00:54
kyrtap: jutro z nim mam wykład ^^
17 kwi 00:54


 Qulka a możesz powiedzieć po co była potrzebna masa, mam mnóstwo pytań
Qulka a możesz powiedzieć po co była potrzebna masa, mam mnóstwo pytań 

 Też mam koło w piątek i Qulka jedyną nadzieją na
zdaną fizykę
Też mam koło w piątek i Qulka jedyną nadzieją na
zdaną fizykę 
 √vx2+vy2 i tak samo z r
√vx2+vy2 i tak samo z r
 ?
?





 Czekajmy na Qulke
Czekajmy na Qulke
 Przecież da wam inne dane...
Przecież da wam inne dane...
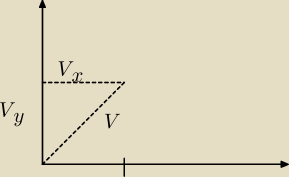 b)
F→=(cos(t), t3)
m=1
takie mam dane wyznaczam najpierw przyśpieszenie z podstawowego prawa fizyki:
b)
F→=(cos(t), t3)
m=1
takie mam dane wyznaczam najpierw przyśpieszenie z podstawowego prawa fizyki:












