Geometria REBI: Zad. 1 dany jest trojkat prostokątny ABC, w którym kąt ACB= 90 stopni. Punkt D lezy na przyprostokatnej AC. Udowodnij, że jeżeli BC=2*CD oraz AD=5*CD, to kąt ABD jest równy 45 stopni.

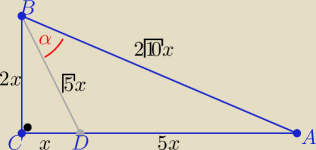Eta: |CD|=x , |BC|=2x , |DA|=5x |CA|=6x , x>0 z tw. Pitagorasa |DB|=√4x²+x²=√5x i |AB|=√4x²+36x²= 2√10x z tw. kosinusów w trójkącie DAB

	5x2+40x2−25x2		1		√2
cosα=		=		=		⇒ α=45o
	2√5x*2√10x		√2		2