Proszę o pomoc :)
mario:
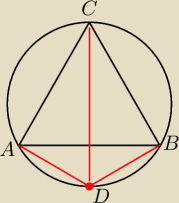
W okrąg wpisano trójkąt równoboczny ABC. Na okręgu wpisano punkt D (różny od punktów A,B,C) i
poprowadzono trzy odcinki DA DB DC. Wykaż że suma długości dwóch krótszych odcinków jest równa
długości odcinka trzeciego. Zależy mi żeby zadanie było rozwiązane z pola trójkąta.
15 kwi 21:59
mario: ...
15 kwi 22:25
mario: ...
15 kwi 23:50
Benny: Czemu z pola? Obierz punkt E(przecięcie CD z AB)
| | 4 | |
DB z pitagorasa, CD jest równe |
| h |
| | 3 | |
15 kwi 23:56
Tadeusz:
16 kwi 00:10
Tadeusz:
punkt D obieramy dowolnie
16 kwi 00:12
mario: To widać, ale dalej nie wiem jak to uzasadnić, że suma AD i DB jest rowna CD
16 kwi 00:12
Tadeusz:
baw się kątami ...polem trójkąta i twierdzeniem cosinusów
16 kwi 00:20
mario: Z twierdzenia cosinusów jest najłatwiej, mam właśnie problem z użyciem w tym zadaniu
rozwiązania z użyciem pól trójkąta.
16 kwi 00:22
Tadeusz:
patrz na kąty
∡BDC=
∡ADC=
16 kwi 00:36
Tadeusz:
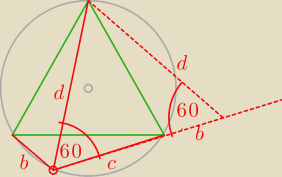
16 kwi 00:47
Eta:
a= |AC|=|AB|=|BC|
Z twierdzenia Ptolemeusza
|AB|*|CD|= |AC|*|BD|+|AD|*|BC|
a*|CD|=a*|BD|+|AD|*a /: a ⇒ |CD|=|BD|+|AD|
c.n.u
16 kwi 00:54
Tadeusz:
On chciał na polach .... teraz pewnie już zauważy
... jeśli rano zajrzy −
16 kwi 00:59
Eta:
"na polach" już wiosnę widać
16 kwi 01:00
Tadeusz:
i nie tylko na polach −
W lesie już kwieciście i gwarno.
16 kwi 01:03
Eta:
U mnie na balkonie gołąb grzywacz wysiaduje młode
16 kwi 01:04
bezendu:
Eta czyli jutro na obiad gołąbki ?
16 kwi 01:06
Eta:
16 kwi 01:07
Tadeusz:
... gołąbki jak gołąbki ... ale na pewno będzie miała upstrzony parapet
16 kwi 01:08
bezendu:
Ale mi chodziło o gołąbki ze słoika
16 kwi 01:09
Tadeusz:
gołąbki ze słoika to tylko dla kawalerów i ... cygańskich psów.
Poważny człowiek tego nie jada −
16 kwi 01:11
Eta:
Dokładnie to miałam pisać
16 kwi 01:12
Eta: No i jeszcze dla
studentów
16 kwi 01:13
Tadeusz:
o parapecie czy o gołąbkach? −
16 kwi 01:13
Tadeusz:
"Poważny" student umie wkupić się w łaski żeńskiego pokoju ... i jada dobrze −
16 kwi 01:15
mario: Pobawię sie tym, zobaczymy czy coś w tym zobaczę. Widze dwa trójkąty rownoboczne.
16 kwi 07:19
mario: Ratunku! Ciagly brak pomyslu na rozwiazanie z uzyciem pol trojkatow.
16 kwi 09:51
mario: Myslalem nad obliczeniem czworokata ABCD na dwa sposoby.
16 kwi 10:40
===:
a czego w tym nie rozumiesz?
Kąty rozumiesz?
16 kwi 10:54
===:
... ciepło ... ciepło −
16 kwi 10:56
===:
jesteś
16 kwi 11:00
===:
1. Wyznacz |AB| za pomocą b i c z tw. cosinusów
|AB|
2=b
2+c
2+bc
2. Pole czworokąta ACBD to suma P
ΔABC+P
ΔABD
| | (b2+c2+bc)√3 | | bc√3 | | √3(b+c)2 | |
Otrzymasz P□ACBD= |
| + |
| = |
| |
| | 4 | | 4 | | 4 | |
3. Pole czworokąta ACBD to suma P
ΔACD+P
ΔCDB
| | √3bd | | √3cd | | √3d(b+c) | |
Otrzymasz P□ACBD= |
| + |
| = |
| |
| | 4 | | 4 | | 4 | |
Porównując
| √3(b+c)2 | | √3d(b+c) | |
| = |
| otrzymasz d=b+c |
| 4 | | 4 | |
16 kwi 11:18
mario: Fajnie, dziękuję. Brakowalo mi wlasnie tego, zastosowania tw cosinow dlatego mi to nie
wychodzilo. Zaraz to sobie przeanalizuje.
16 kwi 11:37
mario: Skad wziales pole trojkata ABD?
16 kwi 12:03
===:
ze wzoru na pole trójkąta
Pytałem Cię wcześniej czy "zaskoczyłeś" z kątami −
16 kwi 12:20
mario: ...?
16 kwi 12:38
mario: aaa... ok juz wiem.
16 kwi 12:39
mario: Bosko! Dzięki wielkie już wszystko rozumiem
16 kwi 12:48
===:
wymęczyłem ... ale może lepiej się utrwali −
16 kwi 13:14