Proszę na teraz:) Emilia: Proszę o pomoc: Znajdź wzór funkcji kwadratowej, o której wiadomo, że prosta y=−1 ma z wykresem funkcji jeden punkt wspólny, a prosta y=−2 przecina ten wykres w punktach (−5,−2) i (1,−2).

AROB: pomogę

Julek:

	−5+1
Xw = (		)=−2
	2

Y_w = −1 −2= 25a − 5b + c −2= a + b + c 0 = −24a +6b ⇒ b= 4a −2 = 5a + c c= −2 − 5a b=4a f(x) = ax² + bx + c f(x) = ax² + 4ax −2 − 5a −1 = 4a −8a − 2 −5a 1 = −9a

	1
a= −
	9

	1		4		13
f(x) = −		x2 −		x −
	9		9		9

Julek:

	−5+1
Xw = (		)=−2
	2

Y_w = −1 −2= 25a − 5b + c −2= a + b + c 0 = −24a +6b ⇒ b= 4a −2 = 5a + c c= −2 − 5a b=4a f(x) = ax² + bx + c f(x) = ax² + 4ax −2 − 5a −1 = 4a −8a − 2 −5a 1 = −9a

	1
a= −
	9

	1		4		13
f(x) = −		x2 −		x −
	9		9		9

Julek: AROB, sorry, ale zaczynając nie widziałem Twojego posta... troche się ociągałem

Eta: To ja podam jeszcze prościej

	−5+1
yw= −1 xw=		= −2 ...... ok
	2

teraz : postać kanoniczna: y = a( x +2)² −1 i podstawiamy np: ( 1,−2) otrzymując: −2= a( 1+2)²−1 9a= −1 => a= −¹₉ zatem: y = −¹₉( x +2)² −1 w treści zadania nie jest powiedziane ,ze ma to być postać ogólna , więc może być i kanoniczna

Bogdan: Można prościej. x_w = −2, y_w = −1, bierzemy jeden z punktów, np. (1, −2) i tworzymy postać kanoniczną:

	1
−2 = a(1 + 2)2 − 1 ⇒ a = −
	9

Jeszcze raz postać iloczynowa:

	1		1		4		13
y = −		(x + 2)2 − 1 ⇒ y = −		x2 −		x −
	9		9		9		9

Eta:

Bogdan: Witaj Eto, telepatia, czy co ?

Eta: Witam ....... byłam pierwsza To nie telepatia, to rutyna

Eta: Ale ,że akurat ten sam punkt( 1,−2)

Bogdan: ale ja mam chochlika a Ty Eto nie (postać iloczynowa, powinno być postać kanoniczna)

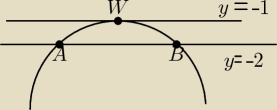
AROB: Y = ax² + bx + c A(−5, −2), B(1, −2)

	xA + xB		−5 + 1
XW =		=		= −2
	2		2

y_W = −1, czyli W(−2, −1) Trzy punkty należące do wykresu podstawiamy do wzoru funkcji kwadratowej tworząc układ 3 równań. A(−5,−2) : −2 = 25a −5b + c B(1, −2) : −2 = a + b + c W(−2,−1): −1 = 4a − 2b + c 25a −5b + c = −2 a + b + c = −2 ⇒ c = −2−a−b 4a −2b + c = −1 25a − 5b − 2 − a − b = −2 4a − 2b −2 −a −b = −1 24a −6b = 0 /:(−6) 3a − 3b = 1 /:3 −4a + b = 0

	1
a − b =
	3

−−−−−−−−−−−−−−−−

	1		1
−3a =		⇒ a = −
	3		9

	1		1		4
−		− b =		⇒ b = −
	9		3		9

	1		4		4
c = −2 +		+		= −1
	9		9		9

	1		4		4
Odp. y = −		x2 −		x −1
	9		9		9

Bogdan: to przez Kubę Wojewódzkiego, którego kątem oka oglądam teraz

Bogdan: O!, AROB też się włączyła, witaj AROB

AROB: Witajcie Eto i Bogdanie. Ja tu spokojnie piszę ( bo też mi Kuba "przeszkadza"), a tu lawina chętnych na to samo zadanie − ale bez zgłoszenia!

Eta: Witaj AROB My z Bogdanem leniwi jesteśmy do takich " długich rachunków " Poszliśmy telepatycznie..... na "skróty"

AROB: Dobranoc WSZYSTKIM !

Eta: Miłych snów AROB