Wyznacz równanie stycznej do wykresu funkcji f w punkcie P Bartuś: Wyznacz równanie stycznej do wykresu funkcji f w punkcie P(x₀,−8). Ile punktów wspólnych z wykresem funkcji f ma ta styczna?

	x2
f(x)=
	2−x

Wyliczyłem f ' (x)= 4x−x² x₀ wyszło mi 6²₅ ale w odpowiedzi jest napisane y=−8, jeden punkt wspólny Nie rozumiem jak rozwiązać to zadanie, proszę o wsparcie

Janek191: Źle policzona pochodna

Bartuś: i wszystko jasne ale czemu nie wyjdzie x₀?

Bartuś:

	4x−x2
ok mam już
	2−x2

Janek191:

	x2
f(x) =		, x ≠ 2
	2 − x

	2x*( 2 − x) − x2*(−1)		4 x − 2 x2 + x2
f'(x) =		=
	( 2 − x)2		( 2 −x)2

	x*(4 − x)
f'(x) =
	( 2 − x)2

Janek191:

	x2
f(x) =		, x ≠ 2
	2 − x

	2x*( 2 − x) − x2*(−1)		4 x − 2 x2 + x2
f'(x) =		=
	( 2 − x)2		( 2 −x)2

	x*(4 − x)
f'(x) =
	( 2 − x)2

Bartuś: mianownik do kwadratu

Janek191:

xo2
	= − 8
2 − xo

x_o² = − 8*( 2 − x_o) = − 16 + 8 x_o x_o² − 8 x_o + 16 = 0 ( x_o − 4)² = 0 x_o = 4

Bartuś: Dzięki

Janek191: a = f '( 4) = 0 P = ( 4 , − 8) − punkt styczności y = a x + b y = b y = − 8 =====

Bartuś: a = ⁰₄ więc co z tym trzeba zrobić?

Bartuś: Ok, dzięki a jak to rozwiązać? Ile punktów wspólnych z wykresem funkcji f ma ta styczna?

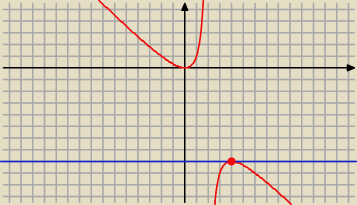
Janek191: Widać na rysunku, że jeden punkt wspólny ( 4 , − 8)

Bartuś: no tak ale czy mozna to jakoś policzyć? Bo na kartkówkach/klasówkach nie wiem czy dam radę narysować dokładny rysunek

Janek191: Styczna ma przeważnie ma jeden punkt wspólny z krzywą. Ta krzywa ma dwie styczne w punkcie O = (0, 0) i w punkcie P = ( 4 , − 8) Można też rozwiązać układ równań :

	x2
y =
	2 − x

y = − 8 ============

Bartuś: Dzięki za pomoc