zbior wartosci tryg
Prezesik: Jak wyliczyć zbiór wartości funkcji f(x) = sin4x + cos4x ?
15 kwi 19:07
ICSP: | | 1 | | 1 | |
sin4x + cos4x = (sin2x + cos2x)2 − |
| (sin2x)2 = 1 − |
| (sin2x)2 |
| | 2 | | 2 | |
15 kwi 19:10
Prezesik: Ok dzięki, ale dalej nie widzę tego zbioru wartości : /
15 kwi 21:19
pigor: ..., to daj se spokój
Prezesik−u z takimi zadaniami
jak nie masz pojęcia o podstawach

np, że |sin2x| ≤ 1.
15 kwi 21:24
YushokU: dokładnie, weź się za coś bardziej elementarnego, a na takie rzeczy przyjdzie czas

15 kwi 21:28
Janek191:
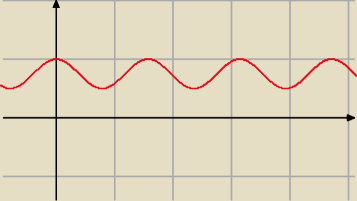
15 kwi 21:33
Prezesik: @Pigor Paradoks polega na tym, że znam te podstawy, ale jeszcze nie mam dobrze wykształconego
myślenia matematycznego i zdarza mi się nie widzieć najprostszych rzeczy w troszkę bardziej
złożonych przykładach, spokojnie stary

Często jak ktoś mi coś wytłumaczy to dopiero widzę
jakie to zadanie jest proste. Ja chcę po prostu rozumieć wszystko tak w 100% a nie 'prawie',
dlatego zadaje tyle pytań

@Janek
Co do tego zadania to dalej nie do końca rozumiałbym z tych obliczeń na górze dlaczego zbiorem
wartości jest akurat <1/2, 1>, a nie może być np. <0, 1/2>?
15 kwi 22:15
pigor: ..., a więc np. tak :
|sin2x| ≤1 /
2 ⇔ 0 ≤ sin
22x ≤1 / : (−2) ⇔ 0 ≥ −
12sin
22x ≥−
12 /+1 ⇔
⇔ 1 ≥1−
12sin
22x ≥ −
12+1 ⇔
120 ≤ 1−sin
22x ≤1, czyli
Z.w.f= <12;1> − szukany
zbiór wartości funkcji f(x)= sin
4x+cos
4x.

15 kwi 22:30
Prezesik: Właśnie o takie coś mi od początku chodziło, dzięki wielkie!

Dla Ciebie to pewnie już w 100%
oczywiste było, dla mnie nie do końca.
15 kwi 22:40
 np, że |sin2x| ≤ 1.
np, że |sin2x| ≤ 1.


 Często jak ktoś mi coś wytłumaczy to dopiero widzę
jakie to zadanie jest proste. Ja chcę po prostu rozumieć wszystko tak w 100% a nie 'prawie',
dlatego zadaje tyle pytań
Często jak ktoś mi coś wytłumaczy to dopiero widzę
jakie to zadanie jest proste. Ja chcę po prostu rozumieć wszystko tak w 100% a nie 'prawie',
dlatego zadaje tyle pytań @Janek
Co do tego zadania to dalej nie do końca rozumiałbym z tych obliczeń na górze dlaczego zbiorem
wartości jest akurat <1/2, 1>, a nie może być np. <0, 1/2>?
@Janek
Co do tego zadania to dalej nie do końca rozumiałbym z tych obliczeń na górze dlaczego zbiorem
wartości jest akurat <1/2, 1>, a nie może być np. <0, 1/2>?

 Dla Ciebie to pewnie już w 100%
oczywiste było, dla mnie nie do końca.
Dla Ciebie to pewnie już w 100%
oczywiste było, dla mnie nie do końca.