trygonometria Kasia1023: Hejka! Prosilabym o pomoc Wyznacz najwieksza i najmniejsza wartosc funkcji f(x)=sin(2x)+cos(2x) w przedziale <0,(pi/2)>

Benny: Jaka jest odpowiedź?

Kasia1023: Wlasnie chcialabym wiedziec

Janek191:

	π
f(x) = sin2 x + cos 2x = √2 sin(		+ 2 x)
	4

Benny: No mi wyszło y_max=√2, a y_min=−1, poprosiłem o odp. ponieważ nie jestem pewny

Kasia1023: Niestety nie mam odpowiedzi, ale twoj wynik chyba sie zgadza bo jak narysowalam sobie wykres w programie to jakos tak wychodzi, to prosilabym o jakies obliczenia i mozliwe wyjasnienie

Janek191:

	π
f(		) = √2
	8

	π
f(		) = = − 1
	2

Janek191:

	π
Jest ok. Oblicz max danej funkcji oraz f(		)
	2

Benny:

	π
@Janek191 jak przeszedłeś do funkcji sin? Mi cały czas wychodzi cos(2x−		)
	4

Kasia1023: Moglby mi ktos to wytlumaczyc dokladniej ?

Janek191: Jest taki wzór

	π		π
sin α + cos α = √2 sin (		+ α) = √2 cos (		− α)
	4		4

dla α = 2 x

Janek191:

	π
Oblicz pochodną funkcji f(x) = √2 sin (		+ 2 x) , a następnie ekstremum
	4

( maksimum ) funkcji f

Benny:

	π
Ok, myślałem, że tylko przy		+−α mogę przejść na kofunkcje
	2

Janek191:

	π		π		π
f'(x) = 2√2 cos (		+ 2 x) = 0 ⇔ cos (		+ 2 x) = 0 ⇔ x =
	4		4		8

oraz

	π
f ''(x) = − 4√2 sin(		+ 2 x)
	4

	π		π
f''(		) < 0 więc f dla x =		przyjmuje maksimum
	8		8

Janek191: @ Kasia 1023 Czy miałaś pochodne ?

Kasia1023: Tak, ale nie mialam pochodnych funkcji trygonometrycznych wiec troche to dla mnie nie jasne, ale dziekuje za pomoc

Janek191: [ sin x] ' = cos x [ cos x] ' = − sin x

Benny: W liceum nie ma pochodnych funkcji złożonych. f(x)=sin2x+cos2x

	π
f(x)=sin2x+sin(		−2x)
	2

	π		π
f(x)=2*sin		*cos(2x−		)
	4		4

	π
f(x)=√2*cos(2x−		)
	4

	π
funkcja przyjmuje największą wartość, gdy cos(2x−		) jest największy tzn.=1
	4

	π
2x−		=0
	4

	π
x=
	8

f(0)=1

	π
f(		)=−1
	2

	π
f(		)=√2
	8

Może tak?

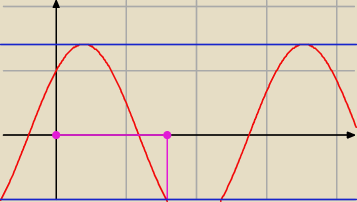
Janek191: Na rysunku dobrze wyszło Proste niebieskie mają równania: y = √2 i y = − 1

	π
Na fioletowo zaznaczyłem przedział < 0,		>
	2

Janek191: Może być