Geometria analityczna analiza matematyczna lawenderr: Wyznacz wymiary prostokąta o maksymalnym polu powierzchni, którego dwa wierzchołki naleza do osi OX , a dwa pozostale, o rzednych dodatnich, naleza do paraboli o rownaniu y=3 −

	1
		x2.
	3

Oznaczylam wspolrzedne punktow:

	1		1
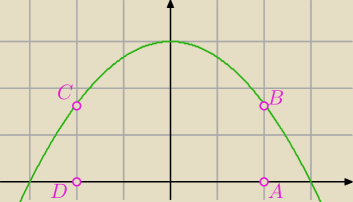
A(xa;0), B(xb;0), C(xc; 3−		xc2), D(xd; 3−		xd2). Po narysowaniu zauwazylam, ze
	3		3

wspolrzedne punktow maja takie zaleznosci: xa=xc i xb=xd i yc=yd. Dalej probowalam wyrazic pole tego prostokata z dlugosci AB i CD ale wychodza mi jakies sprzecznosci..

lawenderr: *z dlugosci AB i AC

Tadeusz: jeśli A=(x_a, 0) B=(x_a, −x_a²/3+3) D=(−x_a,0) |AD|=2x_a |AB|=−x_a²/3+3

	2xa3
S=−		+6xa
	3

S'=−2x_a²+6 S'=0 ⇒ x_a²=3 itd−

lawenderr: Rozumiem do momentu pojawienia sie S − co ono oznacza?

Tadeusz: pole prostokąta

Tadeusz: S=|AD|*|AB|

lawenderr: Dziekuje!

Tadeusz: −