Dwa zadania Blue: zad.1 Wyznacz zbiór wszystkich wartości liczby k, dla których kąt α w trójkącie ABC nie jest ostry. (i mamy tutaj rysunek do tego zadania, gdzie boki trójkąta mają długości 7, 24 i k³−7k+25. Naprzeciw boku k³−7k+25 leży kąt α). Próbowałam z tw. cosinusów, ale wyszła niezbyt przyjemna nierówność... zad.2 W czworokącie wypukłym ABCD punkty E,F,G i H są odpowiednio środkami boków AB,BC,CD, DA

	1		a+b
oraz |EG|=|FH|. Wykaż, że pole tego czworokąta jest nie większe niż		(		)2,
	2		2

gdzie a i b oznaczają długości przekątnych czworokąta.

Qulka: kąt ostry jeśli c²<a²+b² ( k³−7k+25)²<7²+24²=625 k³−7k+25<25 k(k²−7)<0 itd

YushokU: To chyba prostokąt jest jutro nad tym pomyśle

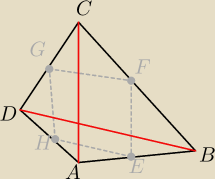
YushokU: miałem pomyśleć jutro, pomyślałem teraz. No i tak. Wiemy, że AE=EB, BF=CF DH=AH Czyli.

AE		AH
	=		czyli HE i DB są równoległe, bo jest to tw. Talesa.
EB		HD

AE		BF
	=		czyli EF i AC są równoległe
EB		FC

Czyli tak będzie dla każdej pary tych boków i przekątnych. Czyli EH||FG i EF||HG, więc to jest równoległobok

	AC		AC		a
No i jeszcze z talesa mamy, że		=		=2 czyli EF i HG są równe
	FE		HG		2

	b
Analogicznie HE i FG są równe
	2

	ab
No i jak przekątne EFGH są równe to będzie to prostokąt, więc jego pole jest równe
	4

No i coś tu trzeba jeszcze pokombinować, ale już coś mamy. Mam nadzieję, że to jest dobrze.

YushokU:

	ab
P=		/*16
	4

16P=4ab 16P≤(a+b)² (a+b)²≥4ab To jest na pewno prawda.

	(a+b)2
czyli		≥P
	16

	a+b		1
czyli P≤(		)2*
	2		4

Widzę, że mi to w ten sposób nie wychodzi, więc prawdą jest również 8P=2ab 8P≤(a+b)² (a+b)²≥2ab

	(a+b)2
P≤
	8

	a+b		1
P≤(		)2*
	2		2

Czyli wyszło. Coś mi się nie podoba ta końcówka.

Blue: YushokU, jesteś geniuszem, dzięki. Sama nie potrafiłam dojść do tego, dlaczego tam jest prostokąt...

YushokU: To dzieło przypadku. Ja nie umiem zbyt dobrze planimetrii Czasami kluczem do zadania jest dokładny rysunek a ta nierówność z polem to chyba wyjdzie ładniej z nierówności między średnią arytmetyczną a geometryczną.

Blue: Nie doceniasz się