 Witam, obliczyłem (wyznaczyłem) monotoniczność funkcji i jej ekstrema lokalne, ale wyniki
wyszły mi trochę podejrzane, zechciałby ktoś zerknąć na poprawność?
Witam, obliczyłem (wyznaczyłem) monotoniczność funkcji i jej ekstrema lokalne, ale wyniki
wyszły mi trochę podejrzane, zechciałby ktoś zerknąć na poprawność?
| x4 | ||
f(x)= | ||
| x−1 |
| x4 | (x4)'(x−1)−(x4)(x−1)' | |||
2* Pochodna f(x)' = ( | )'= | = | ||
| x−1 | (x−1)2 |
| (4x3)(x−1)−(x4)(1) | 4x4−4x3−x4 | 3x4−4x3 | ||||
= | = | |||||
| (x−1)2 | (x−1)2 | (x−1)2 |
| 3x4−4x3 | |
=0 / *(x−1)2 | |
| (x−1)2 |
| 4 | 4 | |||
x=0 3x−4=0 ⇒ 3x=4 ⇒x= | V x=− | |||
| 3 | 3 |
| 1 | 4 | 1 | ||||||||||||||
fmax= | = 5 | ⇒ (− | ;5 | ) | |||||||||||||
| 3 | 3 | 3 |
| 4 | 1 | |||
Fmin = ( | ;5 | ) | ||
| 3 | 3 |
| 4 | 4 | |||
F jest rosnąca dla x∊ (−∞,− | ) V ( | ,∞) | ||
| 3 | 3 |
| 4 | 4 | |||
F jest malejąca dla x∊ (− | ,1)v(1, | ) | ||
| 3 | 3 |
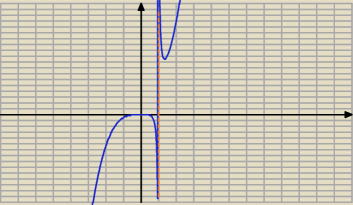
 to nie jest kwadratowe
to nie jest kwadratowe  i chyba się rozpędziłeś przy max i min bo nie może wyjść to samo y bo masz inne mianowniki
i chyba się rozpędziłeś przy max i min bo nie może wyjść to samo y bo masz inne mianowniki