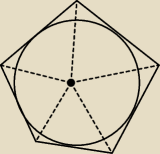
GEOMETRIA hs: Dany jest pięciokąt o polu równym 144 opisany na okręgu o promieniu 6. Cztery boki tego pięciokąta mają długości 5,8; 6; 8,2; 11,6. Oblicz długość piątego boku.

Janek191: P₁ + P₂ + P₃ + P₄ +P₅ = 144 0,5*6*5,8 + 0,5*6*6 + 0,5*6*8,2 + 0,5*6*11,6 + P₅ = 144 17,4 + 18 + 24,6 + 34,8 + P₅ = 144 94,8 + P₅ = 144 P₅ = 0,5*6* x = 144 − 94,8 = 49,2 3 x = 49,2 x = 16,4 ======

hs: Dziękuję. A jeszcze mam pytanie co do okręgów opisanego oraz wpisanego w sześciokąt foremny. Załóżmy, że bok sześciokąta ma długość 'a'. W takim wypadku r=^√3₂a, R=a, P(szesciokata)=3√3a ?

hs: ?

Janek191:

	a2√3
P = 6*		= 1,5 a2√3
	4

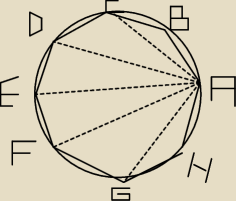
hs: I ostatnie zadanie, którego nie rozumiem. Przekątne ośmiokąta foremnego poprowadzone z jednego wierzchołka podzieliły ten ośmiokąt na sześć trójkątów. Wyznacz miary tych trójkątów.

hs: Pomoze ktos ?