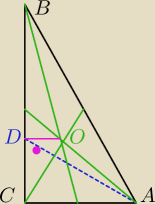
Oblicz miary kątów ostrych szare: Dwusieczna kąta ostrego CAB w trójkącie prostokątnym ABC przecina przyprostokątną w punkcie D. Środkowe trójkąta przecinają się w punkcie O. Odcinek OD jest prostopadły do przyprostokątnej CB. Oblicz miary kątów ostrych tego trójkąta. Jakieś podpowiedzi?

szare: pomocy, nie mam żadnego pomysłu. wydaje mi się, że trzeba coś kombinować z podobieństwem, chyba nie ma innej opcji?

szare: pomocy, nie mam żadnego pomysłu. wydaje mi się, że trzeba coś kombinować z podobieństwem, chyba nie ma innej opcji?

szare: /

+-: Jest takie twierdzenie ośrodkowych. Środkowe trójkąta przecinają się w jednym punkcie. Dzieli on każdą z nich w stosunku 2:1 licząc od wierzchołka. popatrz na tgCAB i tgCAD wiedząc, że CAB=2CAD

Eta:

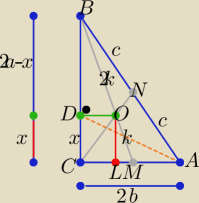
	|BD|		2c		c
Z tw. o dwusiecznej:		=		=
	|DC|		2b		b

środkowe dzielą się w stosunku 2:1 to |OB|=2k i |OL|=k

	|BD|		2k
Z podobieństwa trójkątów LMO i DOB :		=		=2
	|OL|		k

|OL|=|DC|=x

	c
to:		= 2 ⇒ c=2b zatem : |AC|=2b i |AB|=4b i |∡CAB|=α , |∡CBA|=β
	b

	2b		1
cosα=		=		⇒ α= 60o to β= 30o
	4b		2

szare: Fakt, zapomniałam o tym twierdzeniu... Teraz mi głupio. Dziękuję!