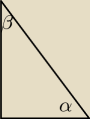
w pewnym trójkącie prostokątnym suma kosinusów kątów ostrych wynosi 2√3/3
oblicz iloczyn sinusów tych kątów
cosα+cosβ=2√3/3
sinα=cosβ
sinα+cosβ=2√3/3 / *2
sin2α+cos2β=2√3/3
i co dalej 
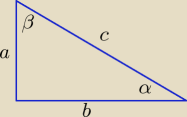
| 2√3 | b | a | 2√3 | 2√3 | ||||||
cosα + cosβ = | ⇒ | + | = | ⇒ a + b = | c | |||||
| 3 | c | c | 3 | 3 |
| 2√3 | 12 | |||
(a + b)2 = ( | c )2 ⇒ a2 + 2ab + b2 = | c2 | ||
| 3 | 9 |
| 12 | 1 | |||
2ab + c2 = | c2 ⇒ ab = | c2 | ||
| 9 | 6 |
| a | b | ab |
| 1 | |||||||||||||||
sinα * sinβ = | * | = | = | = | |||||||||||||||
| c | c | c2 | c2 | 6 |