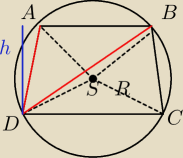
W okrąg o promieniu R=√10 wpisano trapez ABCD, w którym AB||DC. Wiedząc że BD=6 i AD=4√2,
oblicz pole tego trapezu.
Mógłby ktoś mi to sprawdzić? Bo nie jestem pewna co do wyniku..
| 3 | ||
1) z Tw. cos. obliczyłam cos∡ASD = − | ||
| 5 |
| 3 | ||
− | = cos2∡ABD | |
| 5 |
| 3 | ||
− | =2cos2∡ABD − 1 | |
| 5 |
| 2 | |
= 2 cos2∡ABD | |
| 5 |
| 1 | |
=cos2∡ABD | |
| 5 |
| √5 | ||
cos∡ABD = | (ujemny wynik należy odrzucić  ) | |
| 5 |
| √5 | ||
4√22 = 36 = AB2 − 2*AB*6* | ⇒ | |
| 5 |
| 2√5 | ||
AB = | lub AB = 2√5 ( założyłam że to druga podstawa) | |
| 5 |
| h | |
= sin∡ABD | |
| 6 |
| 2√5 | ||
sin∡ABD(z jedynki tryg. )= | ||
| 5 |
| 12√5 | ||
h= | ||
| 5 |
| 1 | 2√5 | 12√5 | ||||
P= | *( | + 2√5 ) * | ||||
| 2 | 5 | 5 |
| 6√5 | 12√5 | |||
P= | * | |||
| 5 | 5 |
| 360 | ||
P= | = 14,4j2 | |
| 25 |