Geometria N1N2: Witam! Pomożecie z jednym zadankiem? Okrąg o: x² + y² − 6√2x + 10 = 0 jest opisany na sześciokącie foremnym ABCDEF. a) Wyznacz współrzędne wierzchołków sześciokąta, wiedząc, że odcięta punktu A jest równa √2. b) Oblicz pole figury F = F₁ − F₂ gdzie F₁ jest sześciokątem ABCDEF, zaś F₂ kołem wpisanym w ten sześciokąt. Prosiłbym o dokładne rozpisanie, abym mógł zrozumieć

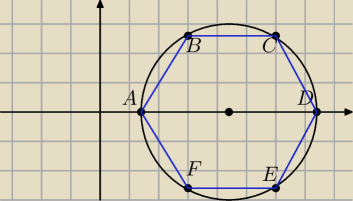
Qulka: A(√2;0) B(2√2;√6) C(4√2;√6) D(5√2;0) E(4√2;−√6) F(2√2;−√6)

Braun: Toś mu Qulka rozpisała

Qulka: Pole F₁ = 12√3 PoleF₂=12π figura = 12(√3−π)

Qulka: a nie widać

Braun: 1:10, że słaby licealista to zrozumie jak to zrobiłaś

Qulka: no ok Okrąg to : (x−3√2)²+y² = (2√2)² sześciokąt foremny to sześć trójkątów równobocznych

Eta:

Braun: Mi nie musisz tego tłumaczyć, ja już dawno po maturze

PW: x2 + y2 − 6√2x + 10 = 0 (x − 3√2)² + y² − (3√2)² + 10 = 0 (x − 3√2)² + y² = 8 Gdyby go przesunąć o wektor [−3√2, 0], to jego obraz miałby śliczne równanie x² + y² = 8. Promień r tego okręgu: r = 2√2. Jednocześnie punkt A przekształci się na punkt A' = (−2√2, 0). Nikt nie zabroni wyznaczyć współrzędne A',B',...F'. Znacznie łatwiej będzie je określić, bo możemy korzystać z symetrii względem początku układu współrzędnych. Aby udzielić odpowiedzi na punkt a) wystarczy dokonać odwrotnego przesunięcia. Może i nie byłoby warto tak się rzucać w te i wewte, ale liczenie b) na pewno będzie "psychologicznie łatwiejsze". W wielu zadaniach po takim łatwym przesunięciu rachunki znacznie się upraszczają.