..
Kevin: oblicz PC i V ostrosłupa prawidłowego czworokatnego o krawędzi podstawy 8 którego sin kąta
nachylenia ściany bocznej do płaszczyzny podstawy wynosi 2/3
13 kwi 22:48
Bogdan:
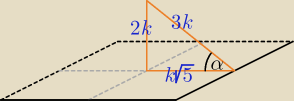
2k
√5 = 8 ⇒ k = ...
| | 1 | |
V = |
| *82*2k = ..., Pc = 64 * 4*k√5*3k = ... |
| | 3 | |
13 kwi 23:01
Kevin: Nie rozumiem Twoich obliczen
13 kwi 23:08
Eta:
13 kwi 23:09
Kevin: Proszę o proste wytłumaczenie
13 kwi 23:12
Bogdan:
To jest najprostsze rozwiązanie.
13 kwi 23:34
dero2005:
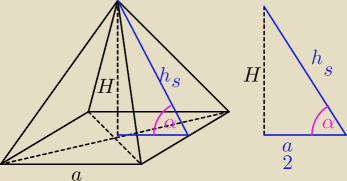
a = 8
| | H | | 2 | | 2 | |
sinα = |
| = |
| ⇒ H = |
| hs |
| | hs | | 3 | | 3 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
z Pitagorasa
(
a2)
2 + H
2 = h
s2
4
2 + (
23h
s)
2 = h
s2
P
c = a
2 + 2a*h
s =
14 kwi 08:33
literat:
Są malarze i malarze pokojów, ale ci też są potrzebni
14 kwi 10:05