Prawdopodobieństwo. aanka: W pierwszej urnie są kule czarne i białe, w drugiej 10 kul niebieskich i 15 kul zielonych, a w trzeciej – 14 kul niebieskich i 7 zielonych. Najpierw losujemy kulę z pierwszej urny, a następnie losujemy kulę z drugiej albo z trzeciej urny w zależności od tego, czy z pierwszej urny wylosowaliśmy odpowiednio kulę białą, czy czarną. Oblicz prawdopodobieństwo wylosowania czarnej kuli z pierwszej urny, jeżeli prawdopodobieństwo wylosowania według opisanego schematu kuli niebieskiej jest takie samo jak zielonej.

aanka:

Kocham matmę, ale nie rozumiem: Pomógłbym Ci, ale nie umiem, mimo, że nie czytałem polecenia.

aanka: Przeczytanie polecenia dużo nie daje

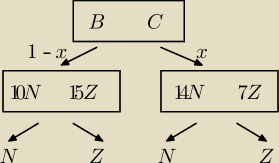
J: x − poszukiwane prawdopodobieństwo

	10		14
P(N) = (1−x)*		+ x*
	25		21

	15		7
P(Z) = (1−x)*		+ x*
	25		21

z warunku: P(N) = P(Z) ..... obliczamy szukane x

aanka: Dziękuje