 I jeszcze jedno zadanie...
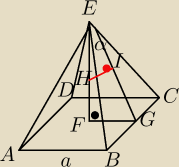
Dany jest prawidłowy ostrosłup czworokątny, którego krawędź podstawy ma długość a i kąt płaski
przy wierzchołku jest α. Oblicz objętość ostrosłupa, którego wierzchołek jest środkiem
wysokości danego ostrosłupa i podstawą jest jedna ze ścian.
Robiłam to tak:
I jeszcze jedno zadanie...
Dany jest prawidłowy ostrosłup czworokątny, którego krawędź podstawy ma długość a i kąt płaski
przy wierzchołku jest α. Oblicz objętość ostrosłupa, którego wierzchołek jest środkiem
wysokości danego ostrosłupa i podstawą jest jedna ze ścian.
Robiłam to tak:
| α | ||
Wyznaczyłam GE z tangensa | i a | |
| 2 |
| EG | a/2 | ||
= | −> z tego wyliczyłam HI | ||
| EH | HI |