Zadanie z Geometrii na płaszczyźnie Kartezjańskiej Słabeusz: Równoramienny trójkąt ABC jest prostokątny i punkt B = (2,4) jest wierzchołkiem kąta prostego. Przeciwprostokątna AC zawiera się w prostej l: 2x + y + 2 = 0. Wyznacz współrzędne wierzchołków A i C Aktualnie to nie potrzebuję takiej pomocy byście policzyli za mnie. Potrzebuję rady , wskazówki bo nie bardzo wiem jak się do tego zabrać. Próbowałem wykombinować coś z odległością(wysokością) , ale nie widzę zależności. Za drugim podejściem próbowałem zrobić równanie prostej przechodzącej przez jakiś punkt na przeciwprostokątnej i przechodzącej przez B , ale bez efektu.

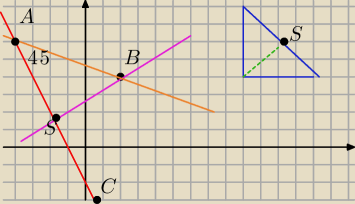
5-latek: Mysle ze z ta wysokoscia jednak dobry pomysl Może tak bym zaczal czerwona to prosta l y=−2x−2 W trojacie prostokątnym równoramiennym wysokość dzieli przeciwprostokatna na dwie rowne części i kat prosty na dwa katy po 45 stopni Wiec napisał równanie prostej prostopadlej do prostej l i przechozdacej przez punkt B Teraz albo wiedzac ze katy przy podsatwie sa rowne wq tym trojkacie sa rowne 45 stopni i znajc przecież wspolczynnik kierunkowy prostel l ze wzoru na kat miedzy prostymi czyli

	a1−a2
tgφ= |		| i wiedzac ze tgφ=1 wyznaczyl wspolczynnik kierunkowy prostej
	1+a1*a2

przecinajaca prosta l pod katem 45 stopni (tej brazowej Znajac wspolczynnik a₂ i wsporzedne punktu B napisał jej rownaie i potem wyznaczyl punkt przecie cia A WIedzac ze punkt S jest srodkiem przreciwprostokatnej i majac wspoprzedne punktu A ze wzoru na srodek odcinka wyznaczyl wspolrzedne punktu C Pewnie można krócej to zrobić Rysunek jest poglądowy . Ma pokazac co liczymy

Słabeusz: Dzięki wielkie