Geometria aanka: Podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC, w którym |AB | = 6, |BC | = |AC | = 10, a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 60. Oblicz objętość tego ostrosłupa.

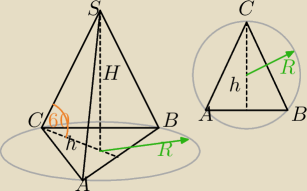
dero2005: AB = 6 BC = CA = 10 h = √BC² − (^AB₂)² = √91

	AB*h
Pp =		= 3√91
	2

	AB*AC*BC
Pp =		= 3√91
	4R

	50√91
R =
	91

H
	= tg60o = √3
R

	50√273
H = R√3 =
	91

	Pp*H
V =		=
	3

aanka: Dzięki wielkie V=50√3j³