arcus DLA AMBITNYCH- ARC: FUNKCJE CYKLOMETRYCZNE− coś dla tych bardziej ambitnych lub wyuczonych proszę o sprawdzenie i skończenie rozwiązania:

	π		π
m) I arc cos x −		I <
	2		6

D=<−1,1>

	π		π
I. arc cos x −		≥0 v II. arc cos x −		<0
	2		2

arc cos x≥arc cos 0 v arc cos x< arc cos 0 x≤0 x>0

	π		π		π
arc cos x <		+		arc cos x<
	6		2		3

	2π
arc cos x<		arc cos x<arc cos 0,5
	3

czy dalej z redukcyjnych? x>0,5

	2π
arc cos x<arc cos (π−		)
	3

	π
x<
	3

x∊Φ odp: x∊(0,5 ; 1>

arc: nikt nie zna funkcji cyklometrycznych? a przecież to forum słynie z wielu geniuszy

arc: AS, Godzio? nie wystarczające wyzwanie, czy nie ten etap edukacji (ja jestem w III klasie LO

Julek: Brawo arc / arcus jesteś geniuszem... To chciałeś przeczytać

arc:

arc: nie. proszę o pomoc... to nowy dział którego jeszcze nie umiem, więc mam pytanie.

arc: ?

paziówna: pierwsza sprawa... Twoja dziedzina to x∊<0,π>, bo to arcusy są

paziówna:

	π		π
|arccosx −		| <
	2		6

	π		π		π		π
arccosx −		<		∧ arccosx −		> −
	2		6		2		6

	π		π		π		π
arccosx <		+		∧ arccosx >		−
	2		6		2		6

	π		π		π		π
arccosx =		+		⇔ cos(		+		) = x
	2		6		2		6

	π		π		π		π
arccosx =		−		⇔ cos(		−		) = x
	2		6		2		6

	π		π		π		1
cos(		+		) = −sin(		) = −
	2		6		6		2

	π		π		π		1
cos(		−		) = sin(		) =
	2		6		6		2

	−1		1
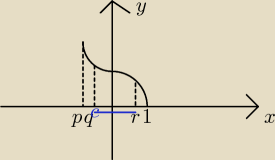
na rysunku: p = −1, q =		, r =
	2		2

	−1		1
więc Twoją odp. są x∊(		;		)
	2		2