okręgi
dipsi: Okręgi x
2+y
2=9 i (x−3)
2+(y−3)
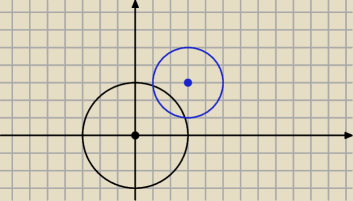
2=4 przecinają się w punktach P i Q. Oblicz sume odległości
punktów P i Q od początku układu wspłrzędnych.
x
2=9−y
2
9−y
2+6x+9+y
2−6y+5=0
6x−6y+23=0
podstawiając do pierwszego równania
delta z tego ujemna
prosze o pomoc
13 kwi 17:06
5-latek:
13 kwi 17:12
J:
druga linijka ... − 6x
13 kwi 17:15
dipsi: ale to nie zmienia mojego równanie
13 kwi 17:19
Mila:
Rozwiązuj tak:
x
2+y
2=9 i
(x−3)
2+(y−3)
2=4
==============
x
2−6x+9+y
2−6y+9=4
x
2+y
2=9
===========odejmuję stronami
−6x+9−6y+9=−5⇔−6x−6y=−23
6y=−6x+23
| | 529 | | 529 | | 529 | | 529*2 | | 529 | |
Δ= |
| −4*2*( |
| −9)= |
| − |
| +72=72− |
| |
| | 9 | | 36 | | 9 | | 9 | | 9 | |
| | 7 | | 2 | | 119 | |
Δ=72−58 |
| =13 |
| = |
| |
| | 9 | | 9 | | 9 | |
dokończ
13 kwi 17:29
dipsi: czy mógłyby to ktoś zzrobić do końca?
13 kwi 17:44
dipsi: z rysunku widać punkt (1;3) i (3;1)
a z obliczeń wychodzą jakieś √119
proszę o pomoc
13 kwi 17:49
Mila:
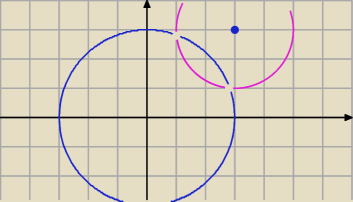
Na rysunku nie masz dokładnych wartości , w tym sensie , że masz punkty kratowe.
Mają byc punkty o wsp. niewymiernych. Chyba, że inne są równania okręgów.
A nie masz odpowiedzi, aby sprawdzić?
13 kwi 18:07
Mila:
Aby obliczyć sumę odległości punktów P i Q od początku układu współrzędnych nie musisz liczyć
wsp. tych punktów
Suma odległości to:
3+3=6
Czy wiesz dlaczego? Patrz na rysunek.
13 kwi 18:12
dipsi: Mila powiedz dlaczego 3+3?
nie widzę tego
13 kwi 18:31
Mila:
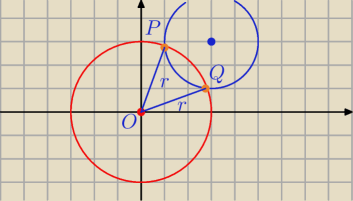
|OP|=r=3
|OQ|=r=3
13 kwi 18:39
dipsi: a ja myślałam że to musi być srodek S odcinka PQ i SO pod kątem prostym do PQ
13 kwi 18:42
Mila:
Trzeba uważnie czytać treść zadania.
14 kwi 15:42

 Na rysunku nie masz dokładnych wartości , w tym sensie , że masz punkty kratowe.
Mają byc punkty o wsp. niewymiernych. Chyba, że inne są równania okręgów.
A nie masz odpowiedzi, aby sprawdzić?
Na rysunku nie masz dokładnych wartości , w tym sensie , że masz punkty kratowe.
Mają byc punkty o wsp. niewymiernych. Chyba, że inne są równania okręgów.
A nie masz odpowiedzi, aby sprawdzić?
 |OP|=r=3
|OQ|=r=3
|OP|=r=3
|OQ|=r=3