Ciąg określony wzorem równy 0 Karolina: Uzasadnij, że tylko jeden wyraz ciągu (a_n) określonego wzorem a_n=n²−(4+√2 )n+4√2 jest równy zero.

Kejt: n²−(4+√2 )n+4√2 = 0 Δ = ... powinna delta wyjść == 0

Karolina: Mi wychodzi ciągle 14−16√2

Kejt: ok, drobna poprawka: (4 + √2)² − 4 * 4√2 = 16 + 8√2 + 2 − 16√2 = 18 − 8√2 i teraz jak wyliczysz n₁ i n₂ to jedno wyjdzie Ci ∊ N a drugie nie. to wystarczy.

pigor: ..., lub np. tak : a_n=0 ⇔ n²−(4+√2)n+4√2=0 i n∊N₊ ⇒ ⇒ n²−4n−n√2+4√2=0 ⇔ n(n−4)−−√2(n−4)=0 ⇔ (n−4)(n−√2)=0 i n∊N₊ ⇔ ⇔ n−4=0 i n∊N₊ ⇔ n=4 , czyli a₄=0 − jedyny wyraz tego ciągu c.n.uz..

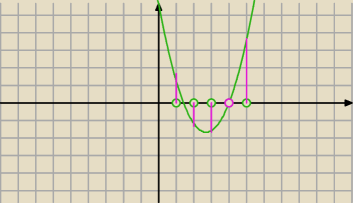
===: wcale delta nie musi być równa 0 Po prostu jeden z pierwiastków nie jest liczbą całkowitą

Kejt: === przecież już się poprawiłam..?

Kejt: I akurat w tym przypadku nie będzie liczbą naturalną. bo nie może być wyraz numer −1..

Karolina: Dziękuję! Ostatecznie n wyszło mi n₁=4 i n₂=√2

pigor: ..., jak zwykle nie ... spadam, szkoda czasu