Analityczna Piotrek: Prosta dana równaniem 2x−y+3=0 przecina okrąg o środku S=(−4,1) w takich punktach A i B że |AB|=12. Oblicz promień tego okręgu.

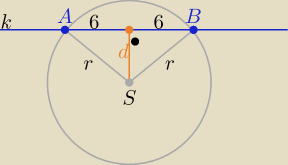
Eta: k: 2x−y+3=0 , S(−4,1) , r>0

	|−8−1+3|
d=		=..........
	√5

r= √6²+d²=..........

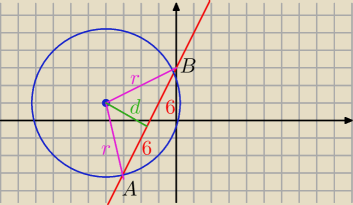
Gustlik: 2x−y+3=0 −y=−2x−3 y=2x+3 Liczę odległość środka okręgu od prostej:

	|Ax0+By0+C|
d=
	√A2+B2

2x−y+3=0, S=(−4,1)

	|2*(−4)−1+3|		|−6|		6√5
d=		=		=
	√22+(−1)2		√5		5

Obliczam promień z Pitagorasa:

	6
r2=(		)2+62
	√5

	36
r2=		+36 /*5
	5

5r²=36+180 5r²=216 /:5

	216
r2=
	5

	216		6√6		6√30
r=√		=		=
	5		√5		5

Eta:

Eta: Nie powinieneś Gustlik podawać gotowca! Wystarczy wskazówka !

Piotrek: Dzięki obojgu!