Punkt D leży na boku AB trójkąta ABC. Udowodnij, że CD>1/2(CA+CB-AB).
Zapalony matematyk: Punkt D leży na boku AB trójkąta ABC. Udowodnij, że CD>1/2(CA+CB−AB).
Mógłby mnie ktoś nakierować? Pozdrawiam
12 kwi 21:03
Ajtek:
Pokombinuj z nierównością trójkąta, pierwsza myśl

12 kwi 21:09
Zapalony matematyk: Kombinowałem, wychodzi mi że CA+CB−AB > 0 czyli 1/2(CA+CB−AB) > 0 ale na tej podstawie raczej
nie mam szans udowodnić tego że CD także jest.
12 kwi 21:11
Zapalony matematyk: Równie dobrze mógłbym udowodnić że skoro 3>0 oraz 5>0 to 3>5, chyba że coś źle rozumiem
12 kwi 21:12
Ajtek:
Z dwoma Δ pokombinuj

.
12 kwi 21:12
Zapalony matematyk: O.. dobry pomysł

Idę pokombinować zaraz dam znać
12 kwi 21:13
Ajtek:
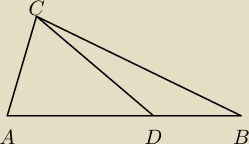
|CD|+|DB|>|BC|
|CD|+|AD|>|AC|
Czy nierówności możemy dodawać stronami bo nie pamiętam

12 kwi 21:16
Zapalony matematyk:
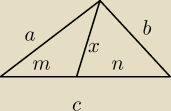
m+n = c
z nierówności trójkąta:
m+x > a
n+x > b
dodaje stronami
2x+m+n > a+b
2x > a + b − c
x > 1/2(a+b−c)
Wyszło, wielkie dzięki

12 kwi 21:17

 .
.
 Idę pokombinować zaraz dam znać
Idę pokombinować zaraz dam znać
 |CD|+|DB|>|BC|
|CD|+|AD|>|AC|
Czy nierówności możemy dodawać stronami bo nie pamiętam
|CD|+|DB|>|BC|
|CD|+|AD|>|AC|
Czy nierówności możemy dodawać stronami bo nie pamiętam 
 m+n = c
z nierówności trójkąta:
m+x > a
n+x > b
dodaje stronami
2x+m+n > a+b
2x > a + b − c
x > 1/2(a+b−c)
Wyszło, wielkie dzięki
m+n = c
z nierówności trójkąta:
m+x > a
n+x > b
dodaje stronami
2x+m+n > a+b
2x > a + b − c
x > 1/2(a+b−c)
Wyszło, wielkie dzięki 