Optymalizacyjne WItam: Oblicz, jaka powinna być dł. promienia podstawy walca o objętości równej V, aby jego pole całkowite było najmniejsze. Prosze o pomooc

Janek191:

	V
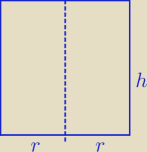
V = Pp*h = π r2*h ⇒ h =
	π r2

zatem

	V
Pc = 2Pp + Pb = 2 π r2 + 2πr*h = 2π r2 + 2πr*
	π r2

	2V
Pc(r) = 2π r2 +
	r

Janek191:

	2V		V
Pc'(r) = 4π r −		= 0 ⇔ π r3 = V ⇔ r = 3√
	r2		π

wtedy

	4 V
Pc''(r) = 4π +
	r3

czyli

	V
Pc ''( 3√		) = 4π + 4π = 8 π > 0
	π

	V
zatem dla r = 3√		funkcja Pc osiąga minimum.
	π

	V
Odp. r = 3√
	π

===============