trapez dipsi: W trapezie ABCD o podstawach AB i CD dane są A(−1,0),D(1,5) oraz punkt przecięcia przekątnych S(2,3). Oblicz współrzędne pozostałych wierzchołków trapezu i pole trapezu jeżeli |DC|=√5

===:

dipsi: można prosić coś więcej do obliczeń bo rysunek już mam ale nie wiem co dalej

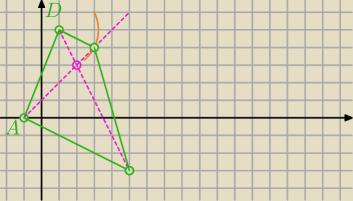
===: ... na rysunku pokazałem jak liczyć − 1) piszesz równania przekątnych 2) z D zataczasz okrąg o promieniu √5 ... punkt przecięcia okręgu z przekątną to C 3) prosta przez DC 4) przez A prostą równoległą do tej prostej 5) przecięcie z drugą przekątną to B

dipsi: mam punkt c=(3;4) prostą CD y=−x+7 prostą AB y=−x−1 i nie potrafię policzyc punktu B

===: sprawdź raz jeszcze te równania Nie podoba mi się ten współczynnik kierunkowy

===: skoro C=(3,4) i D=(1,5) to prosta przez te punkty

	5−4		1
y−5=		(x−1) ⇒ y=−		x+5,5
	1−3		2

Zatem prosta równoległa do niej a przechodząca przez A=(−1,0)

	1		1
y=−		(x+1} ⇒ y=−		x−0,5
	2		2

===: punkt B wyznaczysz dowolnie z układu równań (przecięcie się prostych)

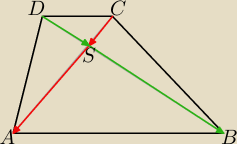
Bogdan: C = (3, 4), S = (2, 3), A = (−1, 0) wektor CS^→ = [−1, −1], wektor SA^→ = [−3, −3] = 3*CS^→ D = (1, 5) a więc SB^→ = 3*DS^→ = 3*[1, −2] = [3, −6] B = (2 + 3, 3 − 6) = (5, −3)