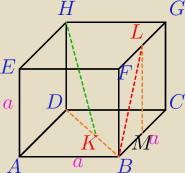
qwerty szklanka ciepłego wina: Punkty K i L są środkami odpowiednio podstawy ABCD i krawędzi F G sześcianu ABCDEFGH . Suma kwadratów długości odcinków HK i BL jest równa 33. Oblicz pole powierzchni całkowitej sześcianu. z trójkąta DKH

	a√2
(		)2 + a2 = HK2
	2

z trójkąta BML

	1
(		a)2 + a2 = BL2
	2

	a√2		3a2
(		)2 + a2 =
	2		2

	1		5a2
(		a)2 + a2 =
	2		4

3a2		5a2
	+		= 33 /*4
2		4

6a² + 5a² = 132 a² = 12 a = 2√3 P = 6* (2√3)² = 72 ?

szklanka ciepłego wina: ?