zad matthew: Cześć. "prawdopodobienstwo' mam takie zadanie: zad1 Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Może ktoś mi to rozwiązać? Jeżeli można to prosiłbym też o wytłumaczenie krok po kroku jak to się robi... bo zupełnie nie wiem jak się za to zabrać

matthew: wiem tylko że |Ω| = 5 chyba

matthew: Może ktoś pomóc?

Kamil: najlepiej jakbyś drzewko rozrysował

Bogdan: Niepotrzebne jest drzewko, zaraz pokażę

Kamil: powinno ci wyjść 0,7

matthew: Nie wiem jakie drzewko, nie wiem jak to zrobić, zaglądałem tuaj na stronie w dział prawdopodobieństwo, ale tego zadania i tak nie rozumiem...

Kamil: jeżeli nie znasz podstaw prawdopodobieństwa to nie wiem czy jest sens tłumaczyć ci to zadanie. byłeś w ogóle na lekcjach z tego

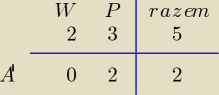
Bogdan: A − wylosowano co najmniej 1 los wygrywający A' − wylosowano puste losy

	5 2		3 2		3
|Ω| =		= 10, |A'| =		= 3, P(A') =
					10

	3		7
P(A) = 1 −		=
	10		10

matthew: troche podstawy znam...

Kamil: fakt można było zrobić zdarzenie odwrotne. Bogdan jesteś w stanie zaradzić coś na taki przykład: x ≤ √4−x2

Kamil: x ≤ √4−x²

krzysiek: x≤2−x 2x≤2/2 x≤1

Kamil: ale ten kwadrat jest tylko nad x

Kamil: 4−x² jest pod pierwiastkiem

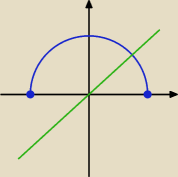
Bogdan: Po lewej stronie jest wykres funkcji y = x, po prawej połowa okręgu y = √4 − x² ⇒ y² = 4 − x² ⇒ x² + y² = 1 Gdzie prosta pokrywa się lub jest poniżej podanej krzywej ?

krzysiek: kwadrat eliminuje pierwiastek i zostaje x≤4−x 2x≤4 x≤2

Kamil: czyli od <−2;√2> tak

Kamil: krzychu jeszcze dziedzina musisz wyznaczyć bo x może być tylko z przedziału (−2;2)

krzysiek: a to ja już wymiękam

leniwiec: x≤√4−x² to wyrażenie pod pierwiastkiem możemy potraktować jakk wartość bezwzględną,tj: x≤|4−x|

Kamil: ale pod pierwiastkiem mamy 4−x² a nie (4−x)²

Bogdan: x ≤ √4 − x², założenie: x∊<−2, 2>, Rozwiązujemy układ równań: 1. y = x 2. x² + y² = 4 (wyżej wdarł się chochlik, nie powinno być x² + y² = 1, ale x² + y² = 4) Założenie: x > 0 i y > 0 x = √2 lub x = −√2 (nie spełnia warunków zadania) Odp.: x∊<−2, √2>