. kleszcz: Punkty A(2, −3) B(4,3) i C(−2, 5) są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta?

Ajtek: Policz długości boków, następnie znajdź współczynnik kierunkowy podstawy. Ostatni krok to wyznaczenie prostej prostopadłej do podstawy przechodzącej przez 3 wierzchołek Δ.

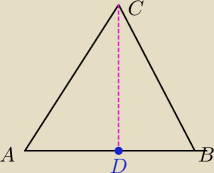
5-latek: AB −podstawa AC i BC to ramiona CD jest to os symetrii trojkata rownoramiennnego . W trojkacie równoramiennym jest tylko jedna os symetrii Jest ona jednocześnie srodkowa AB , wysokoscia trokata , i dwusieczna kata miedzy ramionami To jest rysunek poglądowy Ty nanieś swoje dane na rysunek w układzie wspolrzednych i wyznacz to równanie . napisałem CI wszystko co potrzebne do policzenia

kleszcz: A można tak zrobić wyznaczyć środek odcinka /AB/ − wyszło mi O(3, 0) Wyznaczyć równanie /AB/ i potem wyznaczyć równanie odcinka /DC/ prostopadłego do /AB/ i wyliczyć współczynnik b. ?

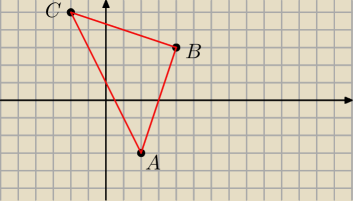
5-latek: Przeciez już z rysunku widać ze podstawa tego trojkata nie będzie AB tylko AC jeśli nie bedziewsz robil rysunkow to przestane CI pomagać .

J: odcinek nie ma równania

	6
współczynnik kierunkowy prostej AB : a =		=3
	2

	1
prostopadła: y = −		x + b ... i przechodzi przez C
	3

	1
−2 = −		*(−2) + b
	3

Janek191: Nie , bo AB nie jest podstawą .

kleszcz: Teraz /AB/ mi wyszło że ma równanie y=3x−9 dobrze mam?

J: szkoda,że nie widziałem Twojego rysunku

kleszcz: aha ok.

5-latek: Czesc J

J: Witaj