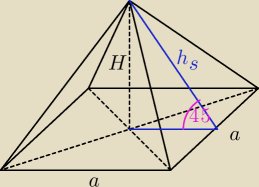
ostrosłup prawidłowy czworokątny Ggg: Ściana boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny jego podstawy pod kątem 45 stopni. Objętość jest równa 343/6. Wyznacz pole całkowite ostrosłupa.

dero2005:

a2H		343
	=
3		6

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

H
	= tg45o = 1
a2

	a
H =
	2

a2*a2		343
	=
3		6

a = 7

a2		a√2
	= cos45o =
hs		2

	√2
hs =
	2

P_c = a² + 2a*h_s =

Ggg: Właśnie z tym miałem problem, skąd to a=7? Jak to zostało wyliczone?

Ggg:

	7√2
chyba hs powinno =		?
	2

dero2005:

a2*a2		343
	=
3		6

a3		343
	=
6		6

a³ = 343 a = ³√343 = 7

a2		√2
	=
hs		2

	a√2		7√2
hs =		=
	2		2

Gapa: tak też liczyłem. Dzięki za naprowadzenie.