. kleszcz: Punkty A(−2, 0) i B(2,0) są wierzchołkami trójkąta równoramiennego ABC o polu 8. Wyznacz współrzędne punktu C.

kleszcz: Wyznaczam równanie prostej /AB/ później środek odcinka /AB/ później wyznaczam równanie odcinka /OC/ prostopadłego do /AB/ podstawiam środek odcinka do wzoru i mam OC to po jaką cholerę jest podane pole 8?

Ajtek: Żebyś wiedział w jakiej odległości od prostej AB leży punkt C .

kleszcz: No tak, ale na cholerę mi to potrzebne do tego zadania .

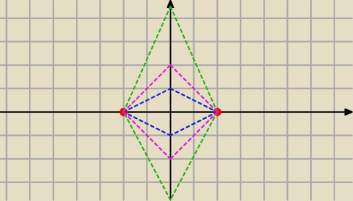
Ajtek: Ponieważ pole Δ ma być 8. Δ równoramiennych o wierzchołkach A i B jest nieskończenie wiele!

kleszcz: ok.

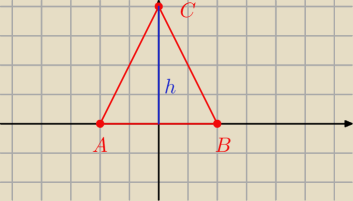
Janek191: Punkty A i B są symetryczne względem osi OY, więc a = I AB I = 2 − (−2) = 4 oraz P = 8 ⇔ 0,5 a*h = 8 ⇔ a*h = 16 ⇔ 4 h = 16 ⇔ h = 4 C = ( 0, 4) ========

Ajtek: Cześć Janek . Dwa rozwiązania są w tym zadaniu przecież C₁(0;4), C₂(0;−4) .

Saizou : a dlaczego twierdzicie że odcinek AB jest podstawą tego trójkąta?

Janek191: @ Ajtek Masz rację

Ajtek: Cześć Saizou, też o tym myślałem, ale uznałem, że to będzie łatwiejsza wersja zadania .

Saizou : Siemasz Ajtek, dawno Cię tu nie widziałem ach....to niedzielne lenistwo

Janek191: Może być jeszcze: C = ( 2, 4) lub C = ( 2 , − 4)

Ajtek: Lub C(−2;4) lub C(−2;−4)

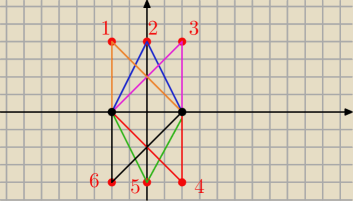
kleszcz: W odpowiedzi jest coś dziwnego C(0, −4) lub C(0, 4) lub C(−2, −4) lub C(−2, 4) lub C(2, −4) lub C(2, 4)

kleszcz: czemu aż tyle tego?

Saizou : Janek jeszcze trochę mało tych rozwiązań bo założyłeś że lABl=lBCl a przecież może być jeszcze lABl=lACl

Janek191: Tak. Ciekawe czy było tyle odpowiedzi do wyboru

Saizou :

kleszcz: ok, czaję już .