.
kleszcz: Punkty A(2, −9) i C(−7, 4) są końcami przekątnej kwadratu ABCD. Oblicz promień okręgu wpisanego
w ten kwadrat.
/AC/ mi wychodzi
√250=5
√10 i mi wychodzi
5√102, zamiast
5√52 jak jest w
odpowiedziach
gdzie mam błąd

?
11 kwi 22:48
Qulka: bo okrąg wpisany to połowa boku a nie przekątnej
11 kwi 22:51
5-latek: Pokaz jak liczysz
11 kwi 22:51
Qulka:
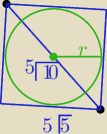
11 kwi 22:53
Qulka: ma dobrze tylko policzył R opisanego
11 kwi 22:53
Marek216: Bok IACI to przekątna kwadratu, tak ? Czyli IACI = a√2 gdzie a to długość boku kwadratu.
Promiń okręgu wpisanego to połowa a, rozumiesz ?
11 kwi 22:54
5-latek: Dobry wieczor
Aniu 
Pozdrawiam

czyli zapomniana dawna czynność robienia rysunku poglądowego do zadania
11 kwi 22:55
kleszcz: aha rzeczywiście masz rację już wiem pomyliłem się jakoś nie wiem czemu

.
11 kwi 22:55
Marek216: Kleszczu ostro zadania atakuje

, jak siedzisz nocami nad tym to na pewno sobie poradzisz na
maturze tylko jak robisz zadania to porządnie analizuj polecenie, i myśl wieloaspektowo
chociażby po to żeby sprawdzić swój wynik.
11 kwi 23:00
kleszcz: Ale jak to w takim razie wyliczyć liczę jedną przekątną
i podstawiam a2=d22
11 kwi 23:00
kleszcz: i z tego a wyliczam czyli odcinek.
11 kwi 23:01
Marek216: d=a√2 to jest ten twój wzór tylko po uproszczeniu.
11 kwi 23:02
Qulka: przekątna kwadratu =a√2
11 kwi 23:02
Marek216: Jak AC policzyłeś dobrz i wyszło 5√10 to robisz tak
Piszesz: 5√10=a√2 Dielisz to przez p{2{ obustronnie o usuwasz niewymierność i wyjdzie a =
(10√5)/2
11 kwi 23:04
5-latek: Liczysz dlugosc przekątnej d
Wiesz ze d=a
√2 to a= .....
11 kwi 23:04
kleszcz: aha no tak kurde, ale powiem wam że chyba z tego dziwnego co wymyśliłem też by się dało

.
11 kwi 23:05
5-latek: 
11 kwi 23:05
kleszcz: Dokładnie z tamtego wyszło 5√5.
11 kwi 23:06
Marek216: a=5√5 i r=1/2 *a ⇒ r =( 5√5)/2
11 kwi 23:06
kleszcz: Dobra ogólnie już wiem o co chodzi dzięki.
11 kwi 23:07
Marek216: n.m.z.c.
11 kwi 23:07
 ?
?

 Pozdrawiam
Pozdrawiam  czyli zapomniana dawna czynność robienia rysunku poglądowego do zadania
czyli zapomniana dawna czynność robienia rysunku poglądowego do zadania
 .
.
 , jak siedzisz nocami nad tym to na pewno sobie poradzisz na
maturze tylko jak robisz zadania to porządnie analizuj polecenie, i myśl wieloaspektowo
chociażby po to żeby sprawdzić swój wynik.
, jak siedzisz nocami nad tym to na pewno sobie poradzisz na
maturze tylko jak robisz zadania to porządnie analizuj polecenie, i myśl wieloaspektowo
chociażby po to żeby sprawdzić swój wynik.
 .
.
