przekroje
paulina: Podstawą ostrosłupa prostego ABCD jest trójkąt prostokątny ABC, którego przyprostokątne mają
długość |AB|= 6 cm, |BC| = 8 cm. Wysokość ostrosłupa jest równa 12 cm. Środki krawędzi AB, BC,
CD i AD wyznaczają płaszczyznę przekroju tego ostrosłupa. Oblicz pole przekroju ostrosłupa tą
płaszczyzną. Bardzo proszę o pomoc..
11 kwi 18:59
paulina:
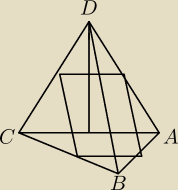
11 kwi 19:04
paulina: Doszłam do tego, że szukanym przekrojem jest równoległobok o bokach długości: 5 cm(połowa AC) i
6,5 cm( połowa BD). Czyli P=5h, gdzie h jest wysokością poprowadzoną na krótszy bok. Proszę o
wytłumaczenie jak policzyć h.. będę bardzo wdzięczna
11 kwi 19:07
paulina: Bardzo proszę o pomoc..
11 kwi 19:24
paulina:
11 kwi 19:41
dero2005:
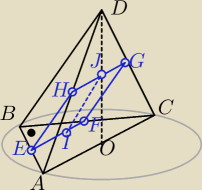
AB = 6
BC = 8
OD = 12
EF =
√(AB2)2 + (BC2)2 = 5
AC =
√AB2 + BC2 = 10
HG = 5
IJ =
√JO2 + (OC2)2 = 3
√5
11 kwi 19:56
paulina: Pole przekroju ma wynieść 6√29
11 kwi 20:08
paulina: ?
11 kwi 20:39
paulina: Ponawiam prośbę
11 kwi 22:01
paulina: pomoże ktoś?
11 kwi 23:18
dero2005:
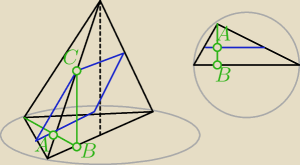
ten ostatni wzór z postu 19:56 jest nieważny (do zapomnienia)
przekrój jest równoległobokiem o długości podstaw równym 5
wysokość równoległoboku to odcinek AC, który policzymy z Pitagorasa
AC =
√AB2 + BC2
| | 6*8 | |
AB to jest połowa wysokości trójkąta podstawy, którego długość wynosi h = |
| = 4,8 |
| | 10 | |
czyli AB = 2,4
BC to połowa wysokości ostrosłupa, czyli 6
| | 6√29 | |
AC = √(125)2 + (305)2 = √104425 = |
| |
| | 5 | |
pole przekroju wynosi
12 kwi 11:25

 AB = 6
BC = 8
OD = 12
EF = √(AB2)2 + (BC2)2 = 5
AC = √AB2 + BC2 = 10
AB = 6
BC = 8
OD = 12
EF = √(AB2)2 + (BC2)2 = 5
AC = √AB2 + BC2 = 10
 ten ostatni wzór z postu 19:56 jest nieważny (do zapomnienia)
przekrój jest równoległobokiem o długości podstaw równym 5
wysokość równoległoboku to odcinek AC, który policzymy z Pitagorasa
AC = √AB2 + BC2
ten ostatni wzór z postu 19:56 jest nieważny (do zapomnienia)
przekrój jest równoległobokiem o długości podstaw równym 5
wysokość równoległoboku to odcinek AC, który policzymy z Pitagorasa
AC = √AB2 + BC2