Wyznacz wszystkie wartości parametru m Sandra: Wyznacz wszystkie wartości parametru m, dla których nierówność jest prawdziwa dla każdej liczby rzeczywistej x: (m−1)x²−2(m−2)x−(m+5)<0

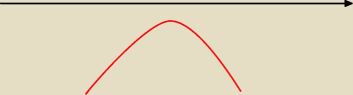
Kejt: musimy mieć taką sytuację jak na rysunku.. jak do niej doprowadzić? wystarczy żeby: a < 0, wtedy parabola jest "smutna" Δ < 0 −−> funkcja nie ma miejsc zerowych, zatem: (m−1) < 0 ⋀ (−2(m−2))²+4(m−1)(m+5)<0 rozwiązaniem jest część wspólna.

Metis: Należy jeszcze sprawdzić kiedy mamy do czynienia z wyrażeniem kwadratowym m−1≠0

Kejt: jeśli m−1<0 to chyba m−1≠0 dla dowolnego m?

Metis: Uczono mnie by zawsze dawać taki komentarz

Kejt: wg mnie to zależy od treści zadania, w tym przypadku jest to bez sensu, bo wiadomo, że: m−1<0 => m−1≠0 miałoby to sens w przypadku np. badania ilości miejsc zerowych w zależności od parametru, wtedy faktycznie trzeba założyć: Δ>0 2 miejsca zerowe i m≠1 Δ==0 jedno miejsce zerowe, lub funkcja jest liniowa(m==1) Δ<0 0 miejsc zerowych i m≠1 ale to tak abstrahując