Mila:
IxI − y = 1
−x + IyI = 1
1) x≥0⇔|x|=x
wtedy mamy układ:
(*) x−y=1
−x+|y|=1
====== dodaję stronami
−y+|y|=2 znowu dwa przypadki
a) y≥0
−y+y=2
0=2 brak rozwiązń
b)y<0
−y+(−y)=2⇔y=−1
podstawiam do (*) x−(−1)=1, x+1=1⇔x=0
(0,−1)
===
2) x<0 wtedy mamy układ
−x−y=1
−x+|y|=1
a) y≥0
−x−y=1
−x+y=1
======−2x=2⇔x=−1 wtedy 1−y=1⇔y=0
Rozw.(−1,0)
=========
b) y<0
−x−y=1
−x−y=1 Układ nieoznaczony, rozwiązaniem jest każda para liczb
spełniająca równanie: y=−x−1 i warunki:
x<0 i −x−1<0⇔
x∊(−1,0)
=====
Odp.
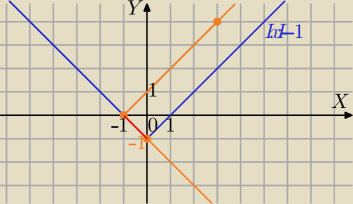
zbiór par (x,−x−1), gdzie x∊<−1,0> ( czerwony odcinek)
PW: Coś mnie kusi, żeby rozwiązać to inaczej.
Prawe strony obu równań są jednakowe, a więc jednakowe muszą być lewe strony:
|x| − y = − x + |y|
|x| + x = |y| + y.
Z definicji wartości bezwzględnej wynika, że obie strony tej równości są liczbami nieujemnymi.
Skoro tak, to obie strony są zerami, albo obie są dodatnie.
Obie strony są zerami, gdy
|x| = − x i |y| = − y,
czyli
(1) x ≤ 0 i y ≤ 0.
Obie strony są dodatnie, gdy
|x| = x i |y| = y,
czyli
x > 0 i y > 0 i 2x = 2y
(2) x = y, x >0, y > 0.
Zastosowanie (1) do badanego układu równań daje dwa jednakowe równania
−x − y = 1, x ≤ 0, y ≤ 0
rozwiązaniem jest zbiór punktów o obu współrzędnych niedodatnich, leżących na prostej
y = − x − 1.
Zastosowanie (2) daje układ równań z warunkiem x > 0 i y > 0:
| | ⎧ | x − y = 1 | |
| | ⎨ | | ,
|
| | ⎩ | −x + y = 1 | |
jest to układ sprzeczny.
Odpowiedź: Rozwiązaniami układu równań są punkty (x, y) o obu współrzędnych niedodatnich,
leżące na prostej y = − x − 1.
Hurra, jest to czerwony odcinek z rysunku
Mili.