Geometria Klodzia: Oblicz cos i sin między wektorami AB i CD gdzie A(2,1), B(5,2), C(4,7), D(1,−5)

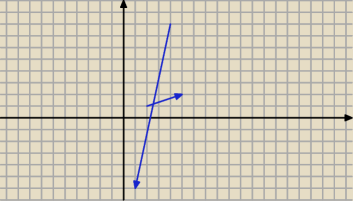
Janek191: → AB = [ 3, 1 ] → CD = [− 3, − 12] Iloczyn skalarny → → AB o CD = 3*(−3) + 1*( − 12) = − 9 − 12 = − 21 Długości wektorów: I AB I = √ 9 + 1 = √10 I CD I = √9 + 144 = √153 = 3√17 więc

	− 21		− 21		7
cos α =		=		= −
	√10* 3√17		3√170		√170

=================================================

	49		121
sin2 α = 1 − cos2α = 1 −		=
	170		170

	11
sin α =
	√170

===============