? Marek: Na okręgu opisano trapez, w którym krótsza podstawa ma długość a, a dłuższa podstawa ˙ tworzy z ramionami kąty o mierze α. Oblicz pole tego trapezu.

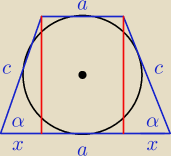
Janek191: Mamy

x
	= cos α ⇒ x = c*cos α
c

b = a + 2 x = a + 2c*cos α oraz a + b = 2 c a + a + 2 c*cos α = 2 c 2a + 2 c*cos α = 2 c / : 2 a + c*cos α = c c − c*cos α = a c*( 1 − cos α) = a

	a		a2
c =		⇒ c2 =
	1 − cos α		(1 − cos α)2

h
	= sin α ⇒ h = c*sin α
c

Pole trapezu P = 0,5*(a + b)*h = 0,5*( a + 2 c*cos α)*c*sinα = 0,5 a*c sin α + c²*sinα*cosα

	a		a2
P = 0,5a*		+		*sinα*cos α =
	1 − cos α		(1 − cos α)2

	a2
= 0,5		*( 1 + U{sin α*cos α){ 1 − cos α}]
	1 − cos α

Janek191: Miało być

	0,5 a2		2sinα*cos α
P =		*[ 1 +		]
	1 − cos α		1 − cos α

	0,5 a2		sin 2α
P =		*[ 1 +		]
	1 − cos α		1 − cos α

Janek191: Obwód L = a + b + 2 c = a + a + 2c*cosα + 2c = 2a + 2c*( cos α + 1) =

	2a		2a*( 1 + cos α)
= 2a +		*(1 + cos α} = 2a +
	1 − cos α		1 − cos α

	1 + cos α
L = 2a*[ 1 +		]
	1 − cos α