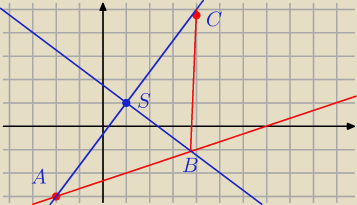
 Np. z. 1
Np. z. 1
| 1 | 7 | |||
x − 3 y − 7 = 0 ⇒ 3y = x − 7 ⇒ y = | x − | |||
| 3 | 3 |
| − 2 + x | − 3 + y | ||
= 1 i | = 1 | ||
| 2 | 2 |
| 4 | ||
a = | ||
| 3 |
| 16 | 15 | 16 | 1 | |||||
b = 5 − 4a = 5 − | = | − | = − | |||||
| 3 | 3 | 3 | 3 |
| 4 | 1 | |||
y = | x − | |||
| 3 | 3 |
| 3 | ||
y = − | x + b1 S = (1, 1) | |
| 4 |
| 3 | ||
1 = − | *1 + b1 | |
| 4 |
| 7 | ||
b1 = | ||
| 4 |
| 7 | ||
y = −U{3}{4] x + | ||
| 4 |
| 3 | 7 | |||
B = ( x , − | x + | ) | ||
| 4 | 4 |
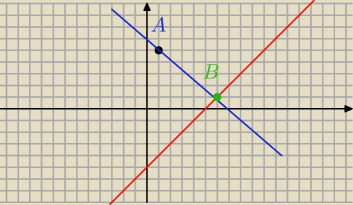 Zadanie nr 3
Ile punktów wspólnych ma styczna do okręgu ?
Pod jakim katem do promienia przechodzi styczna do okręgu
Sa to podstawowe pytania do tego zadania
jeśli już wiemy ze ma jeden punkt wspólny i jest prostopadla do promienia to
1. Odleglosc punktu A od prostej y=x−5 to jest serednica tego okręgu a polowa średnicy to
pronien
(czyli mamy r
2. Żeby obliczyć wspolrzedne punktu B to wyznacz musimy wyznaczyć równanie prostej
prostopadlej do y=x−5 i przechodzącej przez punkt A
Wspolczynnik kierunkowy tej prostej prostopadlej znamy w warunku prostopadlosci prostych
a*a1=−1 wiec a1=−1
Uwaga : Nie bawimy się w zadne obliczanie b bo to dla przedszkolakow (czyli dla mnie
tylko równanie prostej o znaym wspolczynniku kierunkowym i przechodzącej przez dany punktk ma
rownaie
y=a(x−x0)+y0 czyli nasze a = a1=−1 a x0 i y0 to wspolrzedne punktu A
podstaw do wzoru i policz
3. Przyrownujac oba te równania masz wyznaczony punkt B
4. Masz wspolrzedne odcinka AB wiec ze wzoru na srodek odcinka wyznacz wspolrzedne jego
srodka (będzie to jednocześnie srodek okręgu
5 Rownanie okręgu jest takie (x−xs)2+(y−ys)2=r2
Wiec policz
Zadanie nr 3
Ile punktów wspólnych ma styczna do okręgu ?
Pod jakim katem do promienia przechodzi styczna do okręgu
Sa to podstawowe pytania do tego zadania
jeśli już wiemy ze ma jeden punkt wspólny i jest prostopadla do promienia to
1. Odleglosc punktu A od prostej y=x−5 to jest serednica tego okręgu a polowa średnicy to
pronien
(czyli mamy r
2. Żeby obliczyć wspolrzedne punktu B to wyznacz musimy wyznaczyć równanie prostej
prostopadlej do y=x−5 i przechodzącej przez punkt A
Wspolczynnik kierunkowy tej prostej prostopadlej znamy w warunku prostopadlosci prostych
a*a1=−1 wiec a1=−1
Uwaga : Nie bawimy się w zadne obliczanie b bo to dla przedszkolakow (czyli dla mnie
tylko równanie prostej o znaym wspolczynniku kierunkowym i przechodzącej przez dany punktk ma
rownaie
y=a(x−x0)+y0 czyli nasze a = a1=−1 a x0 i y0 to wspolrzedne punktu A
podstaw do wzoru i policz
3. Przyrownujac oba te równania masz wyznaczony punkt B
4. Masz wspolrzedne odcinka AB wiec ze wzoru na srodek odcinka wyznacz wspolrzedne jego
srodka (będzie to jednocześnie srodek okręgu
5 Rownanie okręgu jest takie (x−xs)2+(y−ys)2=r2
Wiec policz 
