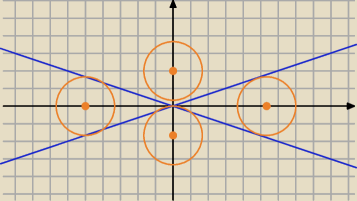
 Są cztery takie okręgi
o1 : (x−1o√10)2+y2=100
o2: (x+10√10)2+y2=100
o3: x2+(y−10√10)2=100
o4: x2+(y+10√10)2=100
Są cztery takie okręgi
o1 : (x−1o√10)2+y2=100
o2: (x+10√10)2+y2=100
o3: x2+(y−10√10)2=100
o4: x2+(y+10√10)2=100
 R=10
S=(a,0) środek okręgu na osi OX
1)
R=10
S=(a,0) środek okręgu na osi OX
1)
| 1 | ||
y= | x⇔x−3y=0 | |
| 3 |
| |a−3*0| | |
=10 | |
| √1+9 |
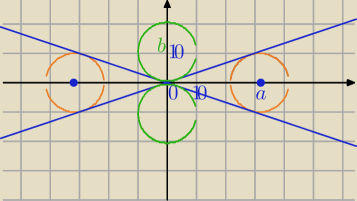 Za wcześnie wysłałam.
cd.
|a|=10√10
a=10√10 lub a=−√10
Równania okręgów: (j.w.)
(x−10√10)2+y2=100
(x+10√10)2+y2=100
2) Analogicznie środki okręgów na OY.
S'=(0,b)
Za wcześnie wysłałam.
cd.
|a|=10√10
a=10√10 lub a=−√10
Równania okręgów: (j.w.)
(x−10√10)2+y2=100
(x+10√10)2+y2=100
2) Analogicznie środki okręgów na OY.
S'=(0,b)
| |0−3b| | |
=10 | |
| √10 |
| 10√10 | ||
|b|= | ||
| 3 |
| 10√10 | ||
x2+(y− | )2=100 | |
| 3 |
| 10√10 | ||
x2+(y+ | )2=100 | |
| 3 |

| 10√10 | ||
okręgi o środkach na osi Oy : S(0,± | ) | |
| 3 |
