Wyznacz dziedzinę mikus: Wyznacz dziedzinę

	log x−1
y=
	√x2−25

Kejt: x²−25 > 0 => x ∊ ... logx − 1 => D: x>0 i część wspólna z obydwu

mikus: a czemu x²−25 jest wzorem skróconego mnożenia?

mikus: x²−25>0 (x−5)(x+5)>0 x>5 i x>−5 ?

blondi: bo masz a²−b² czyli w naszym przypadku x²−5² (bo 5 razy 5 = 25 )

Kejt: pomyliłeś znaki ( > i < ).. jak będzie ostatecznie?

mikus: x=>5 i x=>−5 ale nie wiem

Kejt: zrobiłeś: x > 5 x > −5 tak czy siak, masz błąd w przedziale, narysuj to sobie

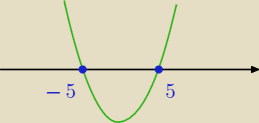
Kejt: kiedy funkcja będzie >0 ?

mikus: tylko nie wiem dlaczego tak?

mikus: bo według mnie powinno być Df: x∊(1,∞)

Kejt: nie rozpędzaj się tak popatrz na mój rysunek, to wykres funkcji x²−25 kiedy będzie ona przyjmowała wartości > 0? (będzie nad osią x)

mikus: tak ale z uwzględnieniem log x−1

Kejt: nadal pudło.

mikus: bo biorąc pod uwagę twój przykład to (−∞,−5)u(5,∞)

mikus: a nie przepraszam (−5,5)

mikus: czyli Df: x∊(1,5) Dobrze

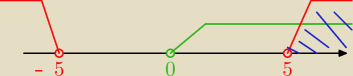
Kejt: tzn. jeśli mówiłeś o tym wykresie z 5 dla całości to jest ok ^^ zielony − log x

mikus: a zielony nie powinien być od 1 ?

mikus: bo tam jest log x−1 czyli: x−1>0 x>1

Kejt: czemu od 1? licznik może być równy 0, zatem ta 1 koło log x nie ma znaczenia. co do samego logarytmu, polecam: https://matematykaszkolna.pl/strona/217.html chyba, ze jest to log (x−1) ..?

mikus: tak to jest log (x−1)

mikus: bo jeśli log x−1 jest bez nawiasu to się nie uwzględnia ?

Kejt: tak to jest jak się nie używa nawiasów...lenistwo wtedy tak, x−1>0 x>1 ale dziedzina całości się nie zmienia

Kejt: jeśli bez nawiasu, to 1 można olać przy liczeniu dziedziny.

mikus: Nie lenistwo roztrzepanie Dziękuję za pomoc

Kejt: Proszę