arkusz Nowa Era YushokU: Potrzebne dużo pomocy Witam, normalnie się dzisiaj załamałem. Skopałem maturkę dość prostą w szkole i drugą dzisiaj w domu, a co najgorsze, mimo, że myślę nad zadaniami to ni w ząb nie portafię ich zrobić Zad. 1 ==> do sprawdzenia Wykaż, że układ równań

⎧	a+b+c+d+e=20
⎩	abcde=320

z niewiadomymi a,b,c,d,e nie ma rozwiązania w zbiorze liczb całkowitych. ODP:Iloczyn pięciu liczb całkowitych jest równy 3²0, co wskazuje na to, że wszystkie liczby a,b,c,d,e są potęgami cyfry 3. Suma pięciu liczb nieparzystych nie może być parzysta, więc ten układ na pewno nie ma rozwiązania w zbiorze liczb całkowitych. (nic innego mi do głowy nie przychodzi, a liczeniem się chyba tego za bardzo robic nie da) Zad.2 ==> do sprawdzenia

	4x2−9
Wyznacz wszystkie wartości parametru p, dla których równanie		+√2=4 ma
	√4x2−12x+9

dwa rozwiązania

(2x−3)(2x+3)
	=4−√2
|2x−3|

rozdzielam na dwa przedziały(pominę) i mam:

	3
−2x−3=4−p√2 dla x<
	2

	3
2x+3=4−p√2 dla x≥
	2

Teraz sobie to narysowałem: i mam p∊<−√2;+∞) Dobrze? Zad.3 ==> tutaj coś pokombinowałem na kartce, niby coś wyszło, ale bezużyteczne, także chyba nie umiem Ustal dla jakich wartości parametru k∊R układ równań

⎧	(x+3)2+(y−2)2=8
⎩	(x−y+1)(x+y−k)=0

ma dokładnie dwa rozwiązania. Zad.4 ==> podpunkt a) mam i jest na pewno ok, ale z b nie mogę sobie poradzić Środkowe AK i BL trójkąta ABC przecinają się w punkcie N. Wierzchołek C leży na okręgu przechodzącym przez punkty K,L,N. a)Wykaż, że ∡KAB=∡ACN i ∡ABL=∡BCN b)Oblicz długość środkowej CM, wiedząc że AB=c Zad.5 ==>teoretycznie mam coś do rozwiązania, ale jest to bardzo niewygodne i nie mam innego pomysłu na zadanie W stożek wpisano kulę, której pole powierzchni jest dwa razy mniejsze niż pole powierzchni calkowitej stożka. Oblicz cosinus kąta nachylenia tworzącej stożka do płaszczyzny jego podstawy oraz stosunek objętości stożka do objętości kuli. Zaraz w poście niżej wstawię propozycję do 5, bo przyda się rysunek Wiem, że dużo tu wstawiłem, ale liczę, że pomożecie mi rozwiązać te zadania i je zrozumieć. Z góry wszystkim serdecznie dziękuję za jakąkolwiek pomoc Pozdrawiam.

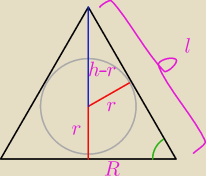
YushokU: Zad.5 P_s=πR(R+l)

	πR(R+l)
Pk=4πr2=
	2

8r²=R(R+l) h=√l²−r²

R
	={r}{√l2−r2−r}
l

r={R √l²−r²}{l+R}

	R2(l2−R2)
8		=R(R+l) − obliczam
	(l+R)2

9R³+3R²l−5Rl²+l³=0 Czyli otrzymuję coś co teoretycznie ma rozwiązanie, ale jest bardzo ciężkie(przynajmniej w LO i dla mnie) do zrobienia. Dzięki za pomoc jeszcze raz!

YushokU: W pierwszym oczywiście abcde=3²⁰

YushokU: W drugim błąd mam w poleceniu: powinno być Wyznacz wszystkie wartości parametru p, dla których równanie

	4x2−9
		+p√2=4 ma dwa rozwiązania.
	√4x2−12x+9

W obliczeniach uwzględniłem, tylko w poleceniu nie dałem

PW: Zadanie 1. Prawie dobrze, ale pominąłeś sytuację, gdy pewne z tych liczb są równe −1 lub 1. O ile 1 się wybroni jako potęga trójki (bo to 3⁰), to już (−1) nie bardzo.

Mila: 1) To Twoja odpowiedź? Jeśli tak to rozumowanie prawidłowe.

YushokU: To mogę w takim razie po prostu tak?: "Iloczyn pięciu liczb całkowitych jest równy 3²⁰, co wskazuje na to, że wszystkie liczby a,b,c,d,e są nieparzyste"

YushokU: tak, moja.

YushokU: Czy może to nieparzyste to zbyt ogólnie?

YushokU: up!

YushokU: Zadanie 5 udało mi się zrobić. Nie zauważylem, że coś może mi się jeszcze tam skrócić (l²−R²)=(l−R)(l+R)

Mila: Zaraz. Podawaj odpowiedzi, jeśli są. To które, teraz zadanie wyjaśniać, pierwsze na razie zostawiamy. Przypomnij, ze trzeba dokończyc.

YushokU: Zad.1==>(chyba już skończone, chociaż czekam na odpowiedź czy jest okej) Zad.2 ==> p∊(−∞,−√2> Zad.3 ==> k∊{−5,−1,3}

	√3
Zad.4 ==> |CM|=c
	2

	1		2
Zad.5 zrobiłem, wychodzi pięknie cosα=		i stosunek równy
	3		1

Mila: w(2) nie widzę w pierwszej linijce parametru p. Rozwiązuję (3)

Mila: 3 (x−y+1)(x+y−k)=0 ⇔ x−y+1=0 lub x+y−k=0⇔ y=x+1 lub y=k−x Podstawiasz do I równania: Dla y=x+1 istnieje jedno rozwiązanie niezależnie od wyboru k Dla y=k−x dajesz warunek Δ=0 wychodzi.

YushokU: aaaa, to o to tu chodziło... Dziękuję, już się za to biorę. W poście 21:29 dodałem poprawkę do zadania nr 2

Mila:

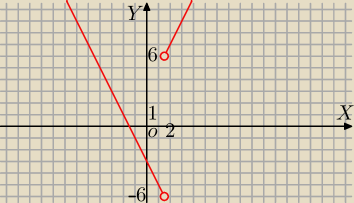
4x2−9		3
	=4−√2*p, x≠
√(2x−3)2		2

(2x−3)*(2x+3)
	=4−√2*p
|2x−3|

	4x2−9
f(x)=		⇔
	√(2x−3)2

	(2x−3)*(2x+3)
f(x)=
	|2x−3|

y=4−√2*p

	3
1) x>
	2

f(x)=2x+3 2)

	3
x<
	2

f(x)=−(2x+3)=−2x−3 Dwa rozwiązania dla 4−√2*p>6⇔ −√2*p>2 /*(−√2) 2p<−2√2 p<−√2 =========

YushokU: OK. Zad.1 − mam Zad.2 − mam Zad.3 − mam Zad.4 − nie mam Zad.5 − mam Także jakby ktoś chciał jeszcze mi dać wskazówkę jak sie zabrać za 4'te b, to będę bardzo wdzięczny A do Ciebie Mila to nie mam słów. Normalnie na zakończenie roku to będę Ci chyba musiał jakieś kwiatki, albo czekoladki podesłać Dziękuję ślicznie

YushokU: Odświeżam

Jacek: Yushoku na pewno wyszło Ci dla 3) zadania k = −5 lub k=−1 lub k=3, bo mi same −5 lub 3 ?

YushokU: Tak, musisz uwzględnić jeszcze ze proste przecinają się w punkcie leżącym na okręgu

Jacek: Tak szczerze to nie rozumiem chyba w ogóle tego 3), bo nawet bym się nie zgodził z zapisem Mili, że dla y=k−x Δ=0. Przy tym założeniu policzyłem k (tzn. podstawiłem do równania okręgu za y, właśnie k−x, ale teraz to wydaje mi się, że skoro w zadaniu proszą by były dokładnie dwa rozwiązania, a samo y=x+1 generuje moim zdaniem dokładnie dwa rozwiązania. No więc chyba należałoby zapisać, że dla y=k−x Δ<0 , a wtedy wychodzi, o ile dobrze liczę: k∊(−∞,−5)∪(3,+∞)

Jacek: YushokU rozumiem, że z do 4) masz punkt b) a brakuje Ci a), czy odwrotnie?

YushokU: Punkt a to mam, za to b jest coś nie tak. Jeszcze wieczorem spróbuje go zrobić, może wczoraj sie zablokowalem. Bo mam pewna koncepcje. 1.laczymy środkowe i mamy dwa trójkąty podobne w skali 2 2. Liczymy przy użyciu chyba tylko pitagorasa i bazujemy na podobieństwie oraz tym ze środkowa dzieli sie w stosunku 2:1 Na razie mam chwile przerwy, spróbuje jeszcze wieczorkiem ale gdyby ktoś rozwiązał to proszę sie podzielić

YushokU: Y=z+1 jest styczna do okręgu wiedz ma jedno stałe rozwiazanie niezależnie od drugiej prostej. Wiec druga prosta musi być styczna lub przecinać sie w wpólnym punkcie z prosta y=x+1 Narysowales sobie to ?

Jacek: Faktycznie, miałem błąd w obliczeniach, jest jedno rozwiązanie przy y=x+1. Czyli pozostaje odnaleźć przy jakich k po podstawieniu za y wyrażeniem k−x do równania okręgu, będziemy mieli punkt styczności pomiędzy okręgiem a prostą z rodziny prostych k−x. I to spełnione jest przy k=−5 lub k=3. Chyba że znów się mylę.

YushokU: Nie, jest dobrze

Jacek: Jak rysuję, to prosta y=−x−1 przecina okrąg w dwóch miejscach, a więc jest chyba źle dla k=−1

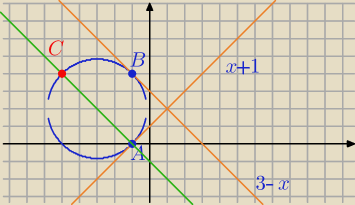
Mila: 1) (x+3)²+(y−2)²=8 y=x+1 A(−1,0) lub (x+3)²+(y−2)²=8 y=k−x k=3 y=3−x B=(−1,4) ============== są dwa rozwiązania sprawdzamy jaką wartość ma k gdy prosta y=k−x przecina okrąg w tym samym punkcie co prosta y=x+1 0=k−(−1)⇔0=k+1⇔k=−1, rozwiązanie układu (x+3)²+(y−2)²=8 y=−1−x (−1,0) (−5,4) Są dwa rozwiązania.

pigor: ..., a ja rozwiążę sobie analitycznie zadanie 2) Wyznacz wszystkie wartości parametru p,

	4x2−9
dla których równanie		+ p√2 = 4 ma dwa rozwiązania.
	√4x2−12x+9

a widzę to tak : −−−−−−−−−−−−−−−−−−−−−−−−−−

	(2x−3)(2x+3)
dane równanie ... ⇒		= 4−p√2 i 2x≠3ma rozwiązanie⇔
	|2x−3|

⇔ (2x+3= 4−p√2 i 2x >3) v (−2x−3= 4−p√2 i 2x< 3) ⇔ ⇔ (2x=1−p√2 i 2x >3) v (2x=p√2−7 i 2x< 3) ⇔ 1−p√2 >3 v p√2−7< 3 ⇔ ⇔ p√2< −2 v p√2< 10 ⇔ 2p< −2√2 v 2p< 10√2 ⇔ ⇔ p< −√2 v p< 5√2 , a więc dokładnie 2 rozwiązania ma ⇔ ⇔ p< −√2 ⋀ p< 5√2 ⇔ p< −√2 ⇔ p∊(−∞ ; −√2) . ...

Jacek: Mila, dla k=−5 chyba też jest OK? W sumie to zgodziłbym się z tym k=−1 o ile można przyjąć, że skoro wychodzi, iż dwa z trzech rozwiązań się pokrywają (−1,0) to w zasadzie mówimy o dwóch rozwiązaniach.

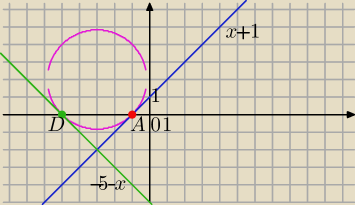
Mila: (x+3)²+(y−2)²=8 y=x+1 lub y=−5−x

YushokU: Odświeżam, próbowałem robić to 4'te, ale nie wychodzi. To do czego doszedłem umieszczę pózniej, bo teraz jestem w sKole na telefonie. Jakby ktoś miał pomysł to proszę o pomoc

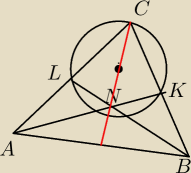
Kacper: Zadanie 4 Środkowe AK i BL trójkąta ABC przecinają się w punkcie N. Wierzchołek C leży na okręgu przechodzącym przez punkty K,L,N. a)Wykaż, że ∡KAB=∡ACN i ∡ABL=∡BCN b)Oblicz długość środkowej CM, wiedząc że AB=c Wystarczy uzasadnić, że trójkąt ABC musi być równoboczny, aby spełnione były założenia zadania

Kacper: Edit. To co napisałem, to bzdura Wcale nic nie musi

YushokU: Nawet nie jest. Ja przez dorysowanie równoległego do podstawy odcinka lk wyznaczyłem poszczególne podobieństwa miedzy trojkatami. Ale jak związać c z środkowa to nie wiem

Kacper: Jak jest równoboczny, to oczywiście spełnione są wszystkie założenia.

Jacek: YushokU jeśli możesz to napisz proszę jak podejść do wykazania tych równości między tymi kątami w zadaniu 4 a).

YushokU: Musisz zauyważyć żę kąty ∡ABL=∡NLK−kąty odpowiadające−widać jak dorysujesz odcinek LK no i ∡NLK=∡NCB, bo są oparte na tym samym łuku I analogicznie druga częśc.

lol:

Jacek: Czyli tak, mamy LK ∥ AB i stąd ∡ABL=∡NLK to kąty odpowiadające, ale nie widzę, aby ∡NLK był oparty na tym samym łuku co ∡NCB. ∡NCB oraz ∡NLK są "oparte" o NK, ale nie te same łuki. No chyba, że czegoś nie widzę.

Kacper: |∡AKL|=|∡KAB| − kąty naprzemianległe a kąty AKL i LCN to kąty wpisane oparte na tym samym łuku.

Jacek: Jakoś nie mogę tego zaakceptować, że się opierają na tym samym łuku. Dla mnie długość łuku dla ∡AKL jest mniejsza niż łuku dla ∡LCN. Oba te kąty "opierają" się o odcinek LN, ale nie te same łuki.

Jacek: A nie, macie rację, zapomniałem o treści i skupiłem się na nie do końca poprawnym rysunku.

Qlka: −23x⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒∊

daras: @YoushokU wspieram Cię mentalnie

YushokU: @daras, a z jakiego to powodu? Ofc miały być naprzemianległe, napisałem odpowiadające. @qlka To jest jakieś wyjaśnienie do zadania? Bo ja tu widzę zażenowanego trójkąta

Kacper: Dobrze, to ja w takim razie podam rozwiązanie podpunktu b) Łatwo pokazać, że punkt P, będący punktem przecięcia odcinka LK i środkowej CM jest środkiem odcinka CM.

	x
Jeśli szukaną długość środkowej oznaczę jako x, to |NP|=		.
	6

Ostatnim krokiem jest skorzystanie z twierdzenia o cięciwach w naszym okręgu. |PL|*|PK|=|PN|*|PC|

c		c		x		x
	*		=		*
4		4		6		2

c2		x2
	=
16		12

	c√3
x=
	2

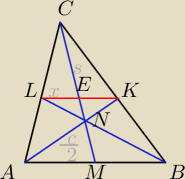
YushokU: o, właśnie wszedłem bo znalazłem rozwiązanie. już myślałem, że nie ma szans żeby to rozwiązać Okazało się, że nie bez przyczyny był ten punkt a) w zadaniu Ja mam tak: s=CM LE=x ΔLKC ≈ ΔABC(k,k,k) w skali k=2

	1		s
|CE|=		CM=
	2		2

	2s
|CN|=
	3

	s
|MN|=
	3

	s
|EN|=|CM|−|CE|−|MN|=
	6

I teraz korzystamy z podpunktu a) ΔLEN≈ΔCEK(k,k,k)

x		s   2
	=
s   6		x

12x²=h² h=2√3x

	1		c		c
ale wiemy że x=		*		=
	2		2		4

	2√3
czyli h=
	4

ufff... Niby proste teraz jak patrze, ale tak to już jest z planimetrią. Użycie wiedzy z gimnazjum w LO i jeszcze są z tym problemy, chyba trzeba na to więcej czasu poświęcić.

YushokU: I dziękuję Kacper za nieco inne podejście, przy okazji poznam nowe twierdzenie

Kacper: Twierdzenie przydatne

YushokU: w ogóle nie wiem skąd mi się to h w rozwiązaniu znalazło, tam gdzie jest h powinno być s