proszę o rozwiązanie Michał: w ostrokątnym trójkącie równoramiennym ABC IACI = IBCI wysokość CD przecięła się z wysokością AE w punkcie S Wysokość AE dzieli ramię BC trójkąta na odcinki BE i EC których długości pozostają w stusunku IBEI : IECI = 1 : 2 a) oblicz sinus kąta EAB b) oblicz stosunek pola trójkata ADS do pola trójkąta SEC

	√6
wynikinto sinα =
	6

stosunek pola trójkata ADS do pola trójkąta SEC = 3 : 8

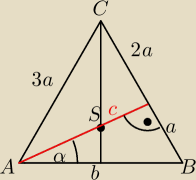Ziom: a) 4a²+c²=9a² c=a*√5 5a²+a²=b² b=a*√6 sinα=a/a√6=√6/6

Michał: dziękuję bardzo

Michał: podpunkt b obliczyłem jeszcze raz dziękuję