k:2x-3y+5=0, m:2x-3y-1=0 Nuwis14: Witam mam taki dylemat. Gdyż mam dwie proste k i m. Mam ich równanie. I mam następujące punkty do zrobienia: b) wyznaczyć równanie okręgu stycznego do prostych k i m c) wyznaczyć równanie okręgu stycznego do prostej m, którego środek jest punktem symetrycznym względem prostej m do punktu należącego do prostej k W punkcie b obliczyłem odległość pewnego punktu na prostej k, po czym obliczyłem odległość tego punktu d do prostej m, podzieliłem przez 2 i to jest mój promień. Moje pytanie brzmi, czy podpunkt c to nie to samo co podpunkt b, bo i w tym przypadku i w tym promieniem jest połowa odległości między prostymi.

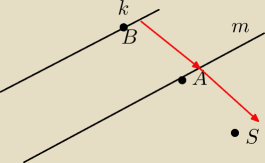
Nuwis14: Chociaż tak jak myślę to skoro środek jest punktem symetrycznym względem prostej m do punktu należącego do prostej k, to punkt na prostej k musimy przenieść względem prostej m o dwa wektory. Wyliczając odległość dowolnego punktu na prostej k do prostej m. Wtedy ten wektor będzie prostopadły do osi m. Wystarczy tą odległość pomnożyć przez 2. Hmm tylko jak wtedy współrzędne odczytać z tego? Bo wtedy była by tylko odległość punktu B, do punktu A razy 2, a żeby mieć współrzędne punktu wartało by mieć jakiś kąt, albo w tym przypadku równanie prostej. Chociaż nie wiem, czy to nie było by źle. Ma ktoś jakiś pomysł? Może przy okazji pomóc z podpunktem b, bo wyszedł mi tak zwany kosmiczny wynik i rozpisywałem to trochę. Na pewno jest jakiś łatwy sposób na rozwiązanie tego.