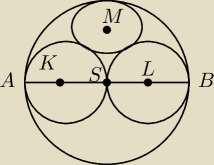
Cztery styczne okręgi Kuba: Cztery okręgi są styczne w sposób przedstawiony na rysunku. Odcinek AB jest średnicą okręgu o środku w punkcie S oraz |AB| = |AS| + |SB|. Wykaż, że stosunek promienia okręgu o środku w punkcie M do promienia okręgu o środku w punkcie S jest równy 1/3

J: x − promień okręg u o środku M r − promienie okręgów o środku K i L R = 2r

	2
mamy: (2r − x)2 + r2 = (x + r)2 .... po wyliczeniu: x =		r
	3

	x		x		1
i dalej		=		=		cnw.
	R		2r		3