pytanie matthew: Cześć. mam pytanie. Kiedy funkcja osiąga wartości nieujemne? Można znaleźć to gdzieś tutaj na tej stronie?

Bogdan: Trzeba rozwiązać nierówność: f(x) ≥ 0

matthew: Rozumiem. Mam taką funkcję f(x)=(x−4)³+(3x−8)² i jest wlaśnie takie pytanie: Kiedy funkcja osiąga wartości nieujemne? Zrobiłem tak: x³ −12X² + 48x − 64 + 9x − 48x + 64 ≥ 0 x³ −12x² + 9x ≥ 0 x(x² − 12x + 9) ≥ 0 x = 0 x² − 12x + 9 z delty wyszły mi 2 m. zerowe: x₁ = 6 − 3√3 x₂ = 6 + 3√3 Może tak być? Dziękuję za odpowiedz

Bogdan: Błąd w rachunkach, zamiast 9x powinno być 9x²

Godzio: może tylko musisz jeszcze napisać przedział w jakim osiąga te wartości

matthew: No tak Czyli na koniec wychodzi x²(x−3)≥0 i miejsca zerowe , to x=0 i x=3 Czyli f osiaga wartosci nieujemne gdy: x=0 i x=3 ?

Bogdan: Dokończ rozwiązywanie nierówności.

matthew: (x−4)³ + (3x−8)² ≥ 0 x³ − 12x² + 48x − 64 + 9x² − 48x +64 ≥ 0 x³ − 3x² ≥ 0 x²(x−3) ≥ 0 x=0 x=3

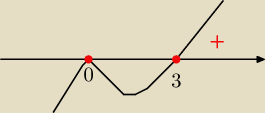
joco: x=0 to pierwiastek dwukrotny rozwiązaniem jest: x€ <3,∞) U {0}

matthew: aaaa zapomnialem o tym zupelnie.... przy nierownosci jeszcze trzeba punkty zaznaczyc na osi prz kwadratowej f byla to parabola, a przy wielomianach wlasnie cos takiego jak krotnosc nie parzysta to przechodzi ,a jak parzysta to odbija... chyba Dzieki za odpowiedzi