Czy odcinek przechodzi przez kwadrat
aliis:
Czy odcinek przechodzi przez kwadrat
Jak obliczyć, jakie wzory, czy dany odcinek przechodzi przez kwadrat?
punkty odcinka A=0, 0 oraz B=3, 3
wierzchołki kwadratu A=1, 2 ; B=2,2 ; C=2, 1 ; D= 1,1
8 kwi 21:02
PW: A = (0, 0) i B = (3, 3). Oznacza to, że odcinek jest zawarty w prostej o równaniu
y = x.
Dokładniej mówiąc, równanie odcinka ma postać
(1) y = x, x∊[0, 3].
Widać, że wierzchołek kwadratu (2, 2) ma współrzędne spełniające równanie (1), a to już
wystarczy, żeby stwierdzić, iż odcinek i kwadrat mają niepustą część wspólną (wolałbym takie
sformułowanie niż "odcinek przechodzi przez kwadrat").
Fatalny błąd autora zadania to oznaczenie tymi samymi symbolami A oraz B różnych obiektów − raz
to są końce odcinka AB, a drugim razem − wierzchołki kwadratu.
9 kwi 15:04
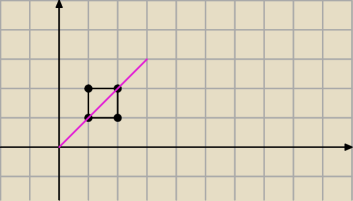
PW: Żeby nie było wątpliwości, czy odcinek tylko "zahaczył o jeden róg" − także D należy do tego
odcinka, a więc odcinek AB zawiera przekątną kwadratu, co zresztą widać na dołączonym obrazku.
9 kwi 15:28
 Czy odcinek przechodzi przez kwadrat
Jak obliczyć, jakie wzory, czy dany odcinek przechodzi przez kwadrat?
punkty odcinka A=0, 0 oraz B=3, 3
wierzchołki kwadratu A=1, 2 ; B=2,2 ; C=2, 1 ; D= 1,1
Czy odcinek przechodzi przez kwadrat
Jak obliczyć, jakie wzory, czy dany odcinek przechodzi przez kwadrat?
punkty odcinka A=0, 0 oraz B=3, 3
wierzchołki kwadratu A=1, 2 ; B=2,2 ; C=2, 1 ; D= 1,1